salut,
Un = (n+1)! / 2^n
- Etudier la monotonie de la suite (Un)
Un+1 - Un = (n+2)! / (2^n+1 ) - (n+1)! /(2^n)
= (n+2)! -2^n+1(n+1)! / 2^n+1
= (n+1)! *[(n+2) -(2^n+2)] / 2^n+1
c'est juste?
La monotonie d'une suite
6 messages
- Page 1 sur 1
Re: la monotonie d'une suite
Je n'ai pas vérifié si c'était juste. Plutôt que calculer la différence entre tes 2 nombres, tu n'as pas envie de calculer le rapport de ces 2 nombres ? En espérant que tu voies où ça peut nous mener.
Re: la monotonie d'une suite
Salut, c'est pas 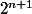 mais seulement 2 (j'ai corrigé en rouge).
mais seulement 2 (j'ai corrigé en rouge).
En effet,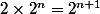
En effet,
yazid47 a écrit:salut,
Un = (n+1)! / 2^n
- Etudier la monotonie de la suite (Un)
Un+1 - Un = (n+2)! / (2^n+1 ) - (n+1)! /(2^n)
= (n+2)! -2(n+1)! / 2^n+1
c'est juste?
Re: la monotonie d'une suite
bonjour,
la suite étant à valeurs strictement positives, on peut calculer le quotient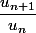 et le minorer par 1 , pour n à partir d'un certain rang. On obtient ainsi le sens de variation de la suite [pourquoi?].
et le minorer par 1 , pour n à partir d'un certain rang. On obtient ainsi le sens de variation de la suite [pourquoi?].
la suite étant à valeurs strictement positives, on peut calculer le quotient
Re: la monotonie d'une suite
j'ai la trouvé :
un+1 - un = (n+2)! - 2(n+1)! / 2^n+1
= (n+1)!(n+2 -2) / 2^n+1
= n(n+1)! / 2^n+1 >= 0
ou comme mathelot dit un+1/un = n+2/2 >1
un+1 - un = (n+2)! - 2(n+1)! / 2^n+1
= (n+1)!(n+2 -2) / 2^n+1
= n(n+1)! / 2^n+1 >= 0
ou comme mathelot dit un+1/un = n+2/2 >1
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
