Devoir maison 1ère

[Snickers]

Bonjour, je voudrais que quelqu'un m'apporte une aide pour mon Devoir Maison que je dois rendre vendredi 24 janvier. Ma prof de maths nous à donner ce DM que mardi et depuis je suis un peut pommé. J'ai déterminé f'(x) mais après pour trouvé les inconnus je ne c'est pas comment faire.

Merci d'avance

[mathelot]

Bonjour, je voudrais que quelqu'un m'apporte une aide pour mon Devoir Maison que je dois rendre vendredi 24 janvier. Ma prof de maths nous a donné ce DM que mardi et depuis je suis un peu paumé. J'ai déterminé f'(x) mais après pour trouver les inconnues je ne sais pas comment faire.

Merci d'avance

bonjour,
que trouves tu pour f'(x) ?

[Snickers]

Bonjour, je voudrais que quelqu'un m'apporte une aide pour mon Devoir Maison que je dois rendre vendredi 24 janvier. Ma prof de maths nous a donné ce DM que mardi et depuis je suis un peut paumé. J'ai déterminé f'(x) mais après pour trouver les inconnues je ne sais pas comment faire.

Merci d'avance

bonjour,
que trouves tu pour f'(x) ?

Pour f'(x)= 2ax+b

[mathelot]

d'accord (je n'arrivais pas à lire l'exposant du trinôme , si c'était 2 ou 3)

Question 1 : l'intersection de la courbe avec l'axe des y donne le point de coordonnées .. ?

sur une courbe, tous les points se repèrent par leurs abscisses

[Snickers]

Question 1 : l'intersection de la courbe avec l'axe des y donne le point de coordonnées (0;1) Non ?

[mathelot]

oui.


une équation de la courbe est


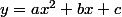
on peut donc remplacer x par 0 et y par 1 pour obtenir une égalité avec a,b,c

si tu les as, écris trois égalités avec a,b et c , on appelle ça un système.

[Snickers]

oui.


une équation de la courbe est


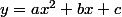
on peut donc remplacer x par 0 et y par 1 pour obtenir une égalité avec a,b,c

Du coup ce qui nous fait: 1=a*0^2+b*0+c
1=c

[mathelot]

oui,c=1.
Que vaut le coefficient directeur de la tangente ? 1 ou 4 (j'ai du mal à déchiffrer)

[Snickers]

oui,c=1.
Que vaut le coefficient directeur de la tangente ? 1 ou 4 (j'ai du mal à déchiffrer)

C passe par le point A(1;2) et admet en ce point une tangente de coefficient directeur 4

[mathelot]

merci bien.

La courbe passe par le point A(1;2). ça nous donne une deuxième égalité avec a et b.

[Snickers]

merci bien.

La courbe passe par le point A(1;2). ça nous donne une deuxième égalité avec a et b.

Oui mais j'ai du mal et je m'embrouille un peut pour savoir comment écrire le système ?

[mathelot]

La courbe passe par le point A(1;2). ça nous donne une deuxième égalité avec a et b.

même chose que précédemment: remplace x par 1 et y par 2 dans l'équation de la courbe.

[Snickers]

La courbe passe par le point A(1;2). ça nous donne une deuxième égalité avec a et b.

même chose que précédemment: remplace x par 1 et y par 2 dans l'équation de la courbe.

Je trouve 2=a+b ?

[mathelot]

L'équation de la courbe est .
Quelle égalité en déduit-on grâce au point A(1;2) ?

[Snickers]

L'équation de la courbe est .
Quelle égalité en déduit-on grâce au point A(1;2) ?

2=a*1^2+b*1+1
0=a+b+1-2
0=a+b-1

[mathelot]

oui, a+b=1.

Pour trouver la 3ème égalité, quelle est le rapport , le lien, la relation (comme tu voudras) entre f'(1) et le coefficient directeur de la tangente à la courbe en A(1;2) ?

[Snickers]

oui, a+b=1.

Pour trouver la 3ème égalité, quelle est le rapport , le lien, la relation (comme tu voudras) entre f'(1) et le coefficient directeur de la tangente à la courbe en A(1;2) ?

Ils ont le même coefficient directeur ?

[mathelot]

oui.
f'(x)=2ax+b

Qu'est est la troisième égalité avec a et b ?

[Snickers]

oui.
f'(x)=2ax+b

Qu'est est la troisième égalité avec a et b ?

Je trouve pas.

[mathelot]

f'(1)=2a+b=4

(on remplace x par 1, puisque le point de tangence est A) et on égalise à 4.