Exercice sur calcul le volume et l'aire d'un domaine

[KysteKXY]

Bonsoir,
S'il vous plaît, j'ai répondu aux autres questions et je suis bloqué à cette 3eme question
On considère dans le domaine U: {(x, y, z); + ; + + 1 }
On note S la surface délimitant U.
1) Décrire U en coordonnées sphériques
2) Calculer le volume de U
3) On note S la surface délimitant U. Calculer l'aire S

[GaBuZoMeu]

Bonsoir,

Qu'est ce qui te bloque ?
Tu as du mal à décrire dans les coordonnées sphérique (distance à l'origine, colatitude, longitude).

Déjà, peux-tu décrire par des mots ? C'est un solide de révolution autour de l'axe des , donc la longitude ne jouera pas de rôle dans la description. Et après ?

[tournesol]

Bonsoir à vous deux .
Quelles coordonnées sphériques ?

[GaBuZoMeu]

Il me semble bien que j'ai indiqué de quelles coordonnées sphériques je parlais. À KristKXY de dire si il ou elle travaille bien avec les mêmes (colatitude ou latitude, par exemple).

[KysteKXY]

1) U en coordonnées sphériques
0 ≤ ≤ 1 ; 0 ≤ ≤/4
0 ≤ ≤ 2
2) calcul du volume
=
3) s'il vous plaît voici où je suis vraiment coincé sur le calcul d'aire S .

[GaBuZoMeu]

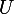
Vu la formule pour l'élément de volume que tu donnes, il semble bien que ton désigne la colatitude. Je ne suis alors pas d'accord avec ton . Fais un dessin en coupe de dans un demi-plan d'axe l'axe des . La condition permet quelles valeurs pour la colatitude ?

Pour la question 3, on est sur la sphère ().
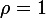
Ne connais tu pas comment l'élément d'aire sur la sphère unité s'exprime par rapport à ? Ça peut d'ailleurs se retrouver facilement : quel est le déplacement infinitésimal sur le méridien correspondant à ? Quel est le déplacement infinitésimal sur la parallèle correspondant à ?

[KysteKXY]

Oui après un petit calcul, j'ai trouvé

[GaBuZoMeu]

Ça ne va toujours pas !
Visiblement, tu n'as pas fait le dessin que j'attendais et qui est celui ci (dans le demi-plan xOz avec x positif ou nul) :

[KysteKXY]

Merci pour le dessin

[GaBuZoMeu]

Merci pour le dessin

Tu n'aurais pas pu le faire toi-même ?

Maintenant, que trouves-tu pour le volume de U ?

Pour l'aire de S, ce que je t'ai écrit plus haut concerne uniquement la partie de S située sur la sphère. Il y a un autre morceau de S, que tu peux deviner d'après le dessin.

[KysteKXY]

Je ne sais pas s'il y'a un problème avec cette intervalle de parce que le volume s'annule entre et .
L'autre surface c'est celle non hachuré et est maintenant différent de 1 je suppose et après on fera la différence des 2 surfaces est-ce celà ?

[GaBuZoMeu]

Je ne sais pas s'il y'a un problème avec cette intervalle de parce que le volume s'annule entre et .

Tu t'es trompé dans ton calcul.

L'autre surface c'est celle non hachuré et est maintenant différent de 1 je suppose et après on fera la différence des 2 surfaces est-ce celà ?

Je me demande si tu comprend bien le dessin. La surface en bleu est une coupe du volume U. La coupe de la surface S, c'est la courbe qui entoure la surface en bleu sur le dessin. La surface S est engendrée par révolution de cette courbe autour de l'axe des z.

[KysteKXY]

Pardon En intégrant le sinus entre et le volume s'annule

Si Je comprends bien c'est une coupe du volume et de la surface qui est seulement représentée dans le plan XOZ et on calcul cette surface en prenant # 1 puisqu'on n'est plus sur la surface de la sphère

[GaBuZoMeu]

Pardon En intégrant le sinus entre et le volume s'annule

Au temps pour moi, c'est bien cet intervalle qui est faux. Reprends le dessin et regarde où est l'angle sur la figure.

Si Je comprends bien c'est une coupe du volume et de la surface qui est seulement représentée dans le plan XOZ et on calcul cette surface en prenant # 1 puisqu'on n'est plus sur la surface de la sphère

Oui c'est un dessin en coupe (ça doit être la troisième fois que je l'écris). La coupe de la surface S se compose d'un arc de cercle et de deux segments de droites. Par révolution autour de l'axe des z, ça donne S comme réunion d'un morceau de cône et d'un morceau de sphère. On calcule séparément la surface du morceau de sphère et celle du morceau de cône, et on ajoute.

[KysteKXY]

Désolé je venais de voir le message.
Oui en mesurant une nouvelle fois l'angle voici ce que j'ai trouvé

[GaBuZoMeu]

Non. Tu vois pourtant bien que l'ouverture du secteur bleu est d'un quart de tour, n'est-ce pas ?

[tournesol]

C'est bien fait pour vous !
Vous n'avez qu'à utiliser la latitude... et l'appeler phi car théta doit rester l'angle polaire dans le plan xoy .

[GaBuZoMeu]

Cette convention (revenant à écrire , où désigne la colatitude et la longitude) est la plus utilisée en pratique, et est celle définie par le standard ISO 80000-2

[tournesol]

Oui mais de mon temps ...
Oui mais je suks un fossile vivant .

[tournesol]

je SUIS