Anneau

[cedric125]

bonsoir besoin d'aide pour cet exercice :
On note Un={z C tel que }
1)démontrer que c'est un sous groupe de C pour la multiplication
2)Montrer que si N* ,m N* et n divise m alors Un Um
3)montrer que si d=pgcm(m,n) alors Ud=Un Um
4)Pour n=5: On pose f:Z------->C tel que est un morphisme de (Z;+) dans (U5;+).determiner kerf

[cedric125]

personne?

[infernaleur]

Bonsoir,
qu'as tu fais pour l'instant, où bloques-tu ?

[capitaine nuggets]

Salut !

1. De manière évidente, l'élément neutre appartient bien à .
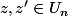
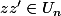
La stabilité du produit l'est tout autant : si alors puisque .
Il reste à montrer la stabilité par passage à l'inverse.

2. Utilise la définition de la divisibilité. L'inclusion est alors évidente

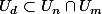
3. L'inclusion est évidente puisque si est le pgcd de et alors est en particulier un diviseur de et , ce qui te permet de conclure d'après la question précédente.
Pour l'inclusion réciproque, utilise le fait que si est le pgcd de et alors on peut trouver deux entiers et premiers entre tels que l'on ait . Or remarque alors que

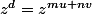
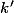
4. Bien qu'il y ait une erreur de recopiage, cette question ne pose aucune difficulté : il faut montrer que réalise un morphisme de dans , c'est-à-dire que , pour tous entiers et . Ce ne sont que des manipulations d'exponentielles complexes niveau terminale
De plus, il faut montrer que . Pour cela, tu peux montrer que est périodique.
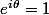
En ce qui concerne le noyau, il suffit juste de se rappeler que si et seulement si .

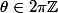
Je te laisse voir tout ça