Convergence

[jeje56]

Bonjour à tous,
On définit la fonction par où et .
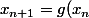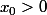
Mon but est de justifier, en utilisant le théorème du point fixe, la convergence de la suite définie par et vers l'unique point fixe de .
n'est pas bornée sur donc je travaille sur puisque au plus à partir du rang et sur cet intervalle.
Puisque n'est pas complet, je dis qu'il existe toujours un intervalle complet où M borne .
Mon raisonnement est-il correct ? Est-il superflu au sens où l'application du théorème serait évidente ?
Merci de votre aide !

[Kolis]

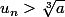
Comment as-tu montré à partir du rang ?
Pourquoi affirmer qu'un ensemble n'est pas complet sans donner la moindre raison ?
Pourquoi affirmer qu'une suite est majorée sans le démontrer ?

Connais-tu exactement l'énoncé du théorème du point fixe ?

[jeje56]

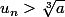
Comment as-tu montré à partir du rang ?
Pourquoi affirmer qu'un ensemble n'est pas complet sans donner la moindre raison ?
Pourquoi affirmer qu'une suite est majorée sans le démontrer ?

Connais-tu exactement l'énoncé du théorème du point fixe ?

Pourquoi être condescendant ?
Pourquoi être condescendant ?
Pourquoi être condescendant ?
Il suffit de me dire que je me trompe en fait...

[tournesol]

ton raisonnement est correct et la borne M n'est pas superflue .

[Kolis]

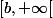
"correct" de dire que n'est pas complet ?

[tournesol]

merci Kolis
j'ai confondu complet et compact . Comme il manque +infini , mon esprit s'est orienté vers le compacifié d'Alexandrov . Donc l'argument du bornage est inutile . jeje56 à confondu comme moi complet et compact .