Expo de matrice

[David.SP]

Bonsoir,

J'ai un probléme sur un calcul d'expo de matrice

on nous donne

Calculer exp(A) en utilisant la série associée
conseil:


Sur ce j'ai calculer A^p sous la forme qui était demandée via les polynômes annulateur et je trouve:



Maintenant je suis bloqué, je n'arrive pas à trouver la limite de la série de et .
Est-ce un probléme dans mon calcul de alpha indice p et beta indice p, sont-ils sous une mauvaise forme ou est-ce qu'on ne peut calculer cette limite.

Merci! je tourne autour de ce probléme depuis deja un petit moment!

[tize]

Tu as essayé en passant par les complexes (formule d'euler) pour exprimer les sommes de sinus et cosinus comme somme de parties imaginaires et réelles de la suite géométrique e ?

[Gato]

Pourquoi cherches tu la limite de ces deux suites ?

Je regarde d'un peu loin mais j'aurais essayé un truc du genre :

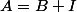
; comme et commutent on peut envisager le binôme de Newton pour calculer

[David.SP]

Merci pour vos réponses.

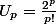
tize, oui j'ai essayé d'y passer, mais le facteur empeche de factoriser la suite géométrique.

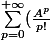Le binôme de Newton n'est pas utile puisque l'on veut utiliser la série l'énoncé ne traitant pas le probléme par ce procédé.

[David.SP]

Je tiens à m'excuser, finalement en utilisant les formules d'Euler, ça sort tout seul...

A bientôt.