Aide exercice kwick trigonométrie

[jvaisretaper]

On considère la fonction def sur R par f(x) = -sin(x)+rac(3)/2

On doit dire si elle est paire ou impaire ou pas sur R
et
on doit donner les solutions de l'équation f(x)=0 sur [0;pi]

Moi je sais que sin est impaire sur R et cos paire sur R mais je ne sais pas comment prouver pour cette fonction si il l'est ou pas, et je comprend pas comment résoudre l'équation
Merci de votre aide!

[Carpate]

3 questions à te poser :
1) f(-x) = f(x) ?
2) f(-x) = - f(x) ?
3) f(x) différent de f(-x) et de -f(-x) ?

[jvaisretaper]

Ok mais je vais pas faire toute la valeur de R pour vérifier
Y a pas un moyen plus simple?

[jvaisretaper]

Ah si en fait il faut juste un contre exemple, pardon
mais pour l'équation je n'y arrive toujours pas

[Carpate]

Moi je sais que sin est impaire sur R et cos paire sur R

donc pour tout

est-ce que c'est égal à f(x), à - f(x) ?

[Carpate]

Résoudre sur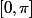 c'est trouver tel que
Et tu dois connaître les valeurs du sinus de quelques angles comme ou savoir les retrouver en plaçant ces angles sur le cercle trigonométrique

[jvaisretaper]

Jai trouvé ça pour f(x) et f(-x):

Sinon j'ai trouvé des contre exemple et la fonction n'est ni paire ni impaire sur R
et pour l'équation j'ai trouvé pi/3 en regardant sur le cercle trigonométrique

[Carpate]

Il n'y a pas besoin de contre-exemple et il faut raisonner pour tout réel x.



Donc et
f ni paire, ni impaire

pour l'équation j'ai trouvé pi/3 en regardant sur le cercle trigonométrique

Justement si tu regardes bien le cercle trigonométrique, tu trouveras une 2ième valeur pour x.

[jvaisretaper]

Ah oui, la deuxième valeur est 2pi/3 je crois
Juste pour savoir le résultat d'une équation sin(x) = quelque chose est en radian ou pas?
Sinon merci beaucoup de ton aide

[Carpate]

C'est indifférent..
Par contre pour dériver (ou intégrer) une fonction trigonométrique, l'angle doit être exprimé en radians.
Le radians est une mesure sans dimension.

[vam]

Bonjour
pas trop d'accord
pour montrer que quelque chose est vrai, on le démontre pour tout x
pour montrer que quelque chose ne fonctionne pas, on prend un contre exemple, et là on aura vraiment démontré que cela ne fonctionne pas

car dire ma démonstration n'aboutit pas, ni dans un cas ni dans l'autre, n'est pas suffisant. On peut en effet rétorquer que si un autre cheminement de démonstration avait été pris, on aurait abouti.

[Carpate]

J'emprunte à Wikipédia ces définitions :
Fonction paire : pour tout x du domaine de définition, f (−x) = f (x)
Fonction impaire : pour tout x du domaine de définition, f (−x) = - f (x)

[vam]

certes, mais ce n'est pas un problème de définition, mais de demonstration mathématique ....