Bonjour j'ai un exercice que je n'arrive pas à faire,pourrez-vous m'aider svp?voilà l'énoncé:
théta est un réel distinct de [smb]pi[/smb] modulo 2[smb]pi[/smb] et:
t=[exp(i*[smb]theta[/smb]/2)-exp(-i*[smb]theta[/smb]/2)] /[exp(i*[smb]theta[/smb]/2) + exp(-i*[smb]theta[/smb]/2 )]
1°) Calculer (2t)/(1+t²) , (1-t²)/(1+t²) et (2t)/(1-t²) en fonction des lignes trigonométriques de [smb]theta[/smb].
2°) Prouvez que :
sin[smb]theta[/smb] = [2tan([smb]theta[/smb]/2)]/[1+tan²([smb]theta[/smb]/2)]
cos[smb]theta[/smb]=[1-tan²([smb]theta[/smb]/2)]/ [1+tan²([smb]theta[/smb]/2)]
tan[smb]theta[/smb]= [2tan([smb]theta[/smb]/2)]/ 1-tan²([smb]theta[/smb]/2)]
Pour la 1ere question j'ai trouvé ces résultats suivant:
(2t)/(1+t²)=[2tan([smb]theta[/smb]/2)]/ [1+(tan[smb]theta[/smb]/2)²}
(1-t²)/(1+t²)=[1-tan²[smb]theta[/smb]/2]/ [1+tan²[smb]theta[/smb]/2]
(2t)/(1-t²)=[2tan([smb]theta[/smb]/2)]/ [1-(tan²[smb]theta[/smb]/2)]
Je n'arrive pas à prouver.
Nombre complexe - un exercice
11 messages
- Page 1 sur 1
Alors je suis partie (je sens que je vais me rendre compte au fur et à mesure que je me suis trompée, mais tant pis... :marteau: ):
Je note X = .
.
2t =}{e^X+e^{-X}})
Et 1+t² = 1 +^2}{(e^X+e^{-X})^2}) =
= ^2 + (e^X-e^{-X})^2}{(e^X+e^{-X})^2}) =
= ^2}) = 2*
= 2*^2})
Donc = (les 2 s'annulent qinsi que le dénominateur de 2t)
= (les 2 s'annulent qinsi que le dénominateur de 2t) (e^X+e^{-X})}{e^{2X}+e^{-2X}}) .
.
Le numérateur est une identité remarquable: (a+b)(a-b) = a²-b², donc:
=
Or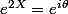 , donc:
, donc:
=
Ensuite, tu développes en cos + i sin
+ i sin  , et tu retrouves mon résultat.
, et tu retrouves mon résultat.
Je note X =
2t =
Et 1+t² = 1 +
Donc
Le numérateur est une identité remarquable: (a+b)(a-b) = a²-b², donc:
=
Or
=
Ensuite, tu développes en cos
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
