Bonjour à tous
J'ai besoin d'aide sil vous plait
Montrer qu'il n'existe pas des entiers naturel x,y,z
Non null telque:
x/y+y/z+z/x=1
J'ai essayé plusieurs fois mais chaque fois j'ai commis des fautes
Merci d'avance
Algébre
7 messages
- Page 1 sur 1
Re: Algébre
Bonjour,
On peut réduire au même dénominateur :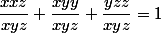
Cordialement,
--
Mateo.
mehdisenpai23 a écrit:
On peut réduire au même dénominateur :
Cordialement,
--
Mateo.
Re: Algébre
Bonjour ;
Si tu poses :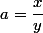 ;
; 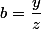 et
et 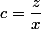 ; alors tu auras :
; alors tu auras : 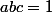 .
.
Si de plus tu supposes que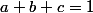 alors tu peux conclure via une inégalité arithmético-géométrique .
alors tu peux conclure via une inégalité arithmético-géométrique .
Si tu poses :
Si de plus tu supposes que
Re: Algébre
mehdisenpai23 a écrit:Mateo . Tu peux m'expliquer plus que ça car j'ai essayé deja cette methode
Re: Algébre
Supposons que 0 < x ≤ y ≤ z,
peux-tu démontrer qu'une des trois fractions x/y , y/z ou z/x est plus grande ou égale à 1 et que les deux autres sont strictement positives, puis conclure ?
Si on avait supposé un autre ordre pour x, y et z, peux-tu arriver à la même conclusion ?
Cordialement,
--
Mateo.
peux-tu démontrer qu'une des trois fractions x/y , y/z ou z/x est plus grande ou égale à 1 et que les deux autres sont strictement positives, puis conclure ?
Si on avait supposé un autre ordre pour x, y et z, peux-tu arriver à la même conclusion ?
Cordialement,
--
Mateo.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
