EXERCICE FACULTATIF : integrales

[Imane2010gazri]

Salut, voici l'exercice:

Soit a>1;
f une fonction dérivable sur [1;a]
Et f' continue sur [1;a]
Montrer que:
$\displaystyle \int_{1}^{a} f'(t)[t] \, \mathrm{d}t$ = [a]f (a)-\sum_{k=1}^{a}{f (k)}
[a] la partie entière de a
Merci pour votre aide!

[Imane2010gazri]

J ignore pourquoi est ce que les formules n apparaissent pas...

[mathelot]

Salut, voici l'exercice:

Soit a>1;
f une fonction dérivable sur [1;a]
Et f' continue sur [1;a]
Montrer que:

[a] la partie entière de a
Merci pour votre aide!

bonjour,
on peut découper l'intervalle d'intégration:
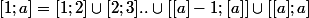
sur lesquels la partie entière de t est constante

NB: pour les formules LaTeX, les encadrer par des balises [ tex] ..[/tex] à la place des dollars