Convergence dominée

[Flashtag]

Bonjour je bloque à cette question
On demande de démontrer que

Avec la question précédente on a montré que

Il suffit de montrer que

Mais c’est compliqué à réaliser comment faire sinon

[Kolis]

Montre que tu peux intégrer la fonction (intégration(s) par parties) sur .
Puis justifie la limite en 1 pour la série.

Ou directement l'intégration terme à terme de sur si tu as le théorème à ta disposition.

[Flashtag]

J’ai cherché à appliquer le théorème d’integration terme à terme .
J’ai posé sur ]0,1] j’ai montré que la fonction est prolongeable par continuité en 0 . J’ai ensuite montré qu’il y avait convergence simple puis normale sur tout l’intervalle d’où la convergence uniforme . Ainsi le théorème s’applique et on a le résultat mais j’ai pas compris la première méthode pourquoi faire une ipp sur la fonction donnée ?

[Kolis]

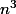
Comment as-tu fait apparaître les au dénominateur dans la formule finale ?

[Flashtag]

Il apparaît naturellement lorsque tu applique le théorème d’integration terme à terme et tu fais une intégration par partie sur