Bonjour à tous ! J’aurais besoin d’aide pour une étude de suite définie par une relation de récurrence telle que :
U0= 1
U1=0
Un+2 = -Un+1 + 2Un + 3
Pour essayer de faire apparaître du second ordre (sans le +3 qui nous en est en posant une nouvelle suite de type Vn= Un+...), j’ai essayé de trouver un point fixe mais j’aboutis a une contradiction (0=3). Comment faire s’il n’existe pas de en point fixe ?
Merci pour votre réponse !
Problème suites récurrentes linéaires d’ordre 2
9 messages
- Page 1 sur 1
Re: Problème suites récurrentes linéaires d’ordre 2
Bonjour,
Point fixe de quoi ? Tu as juste besoin d'une suite particulière vérifiant la relation de récurrence complète (avec le +3). J'ai l'impression que tu cherches une telle suite qui soit constante, mais bien sûr ça ne marche pas.
Je vois par contre une suite non constante, très simple, qui marche bien. Après, par soustraction de cette suite solution particulière de la récurrence, tu es ramené bien sûr à une récurrence linéaire homogène.
Point fixe de quoi ? Tu as juste besoin d'une suite particulière vérifiant la relation de récurrence complète (avec le +3). J'ai l'impression que tu cherches une telle suite qui soit constante, mais bien sûr ça ne marche pas.
Je vois par contre une suite non constante, très simple, qui marche bien. Après, par soustraction de cette suite solution particulière de la récurrence, tu es ramené bien sûr à une récurrence linéaire homogène.
Re: Problème suites récurrentes linéaires d’ordre 2
dans ce cas tu cherche une solution de la forme (an) et a=1 convient .
ta solution générale est de la forme A(-2)^n+n+B , les constantes étant déterminées par les conditions initiales .
ta solution générale est de la forme A(-2)^n+n+B , les constantes étant déterminées par les conditions initiales .
Re: Problème suites récurrentes linéaires d’ordre 2
on a une équation de la forme  a , b , c , d complexes , a non nul.
a , b , c , d complexes , a non nul.
on cherche à priori une solution constante . ça ne marche pas lorsque a+b+c=0
on cherche alors une solution de la forme kn .ça na marche pas lorsque 2a+b=0
Dans ce cas on cherche une solution de la forme et ça marche car a est non nul .
et ça marche car a est non nul .
on cherche à priori une solution constante . ça ne marche pas lorsque a+b+c=0
on cherche alors une solution de la forme kn .ça na marche pas lorsque 2a+b=0
Dans ce cas on cherche une solution de la forme
Re: Problème suites récurrentes linéaires d’ordre 2
GaBuZoMeu a écrit:Bonjour,
Point fixe de quoi ? Tu as juste besoin d'une suite particulière vérifiant la relation de récurrence complète (avec le +3). J'ai l'impression que tu cherches une telle suite qui soit constante, mais bien sûr ça ne marche pas.
Je vois par contre une suite non constante, très simple, qui marche bien. Après, par soustraction de cette suite solution particulière de la récurrence, tu es ramené bien sûr à une récurrence linéaire homogène.
La suite non constante donc tu parles doit elle faire disparaître le +3 ? En gros c’est pour tomber sur du second ordre classique, par exemple avec an = Un - 3 ?
Désolée de si peu comprendre mais on a pas vraiment fait d’exemples comme ça en cours..
merci pour votre réponse
Re: Problème suites récurrentes linéaires d’ordre 2
tournesol a écrit:on a une équation de la formea , b , c , d complexes , a non nul.
on cherche à priori une solution constante . ça ne marche pas lorsque a+b+c=0
on cherche alors une solution de la forme kn .ça na marche pas lorsque 2a+b=0
Dans ce cas on cherche une solution de la formeet ça marche car a est non nul .
D’accord je vois un peu ce que tu veux dire. Ce n’est pas la même technique que le message précèdent non ? Ici k est à déterminer avec les CI ? Merci d’avance
Re: Problème suites récurrentes linéaires d’ordre 2
Petite idée de ma part : Et si je pose Vn = Un+2 -3, et que je retire 3 à tous les membres de droite, ça pourrait marcher non ?
Merci
Merci
Re: Problème suites récurrentes linéaires d’ordre 2
Tournesol t'a donné explicitement une suite vérifiant la relation de récurrence complète ! Ne l'as-tu pas vue ?
Re: Problème suites récurrentes linéaires d’ordre 2
Soit 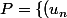 / \forall n \, u_{n+2}+u_{n+1}-2u_n=3\}) et
et 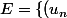 / \forall n \, u_{n+2}+u_{n+1}-2u_n=0\})
La suite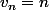 appartient à P.
appartient à P.
E est un -espace vectoriel de dimension 2
-espace vectoriel de dimension 2
On cherche des éléments de E de la forme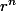
On résout l'équation d'inconnue réelle r.
d'inconnue réelle r.
r=1 ou r=-2
 \in E \Leftrightarrow \exists (A;B) \in \mathbb{R}^2 \qquad u_n=A(-2)^n+B1^n)
P est un plan affine de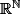
 \in P \Leftrightarrow (u_n-v_n) \in E)
la forme générale des éléments de est de la forme
est de la forme
^n +B 1^n)
i.e, un point plus une combinaison linéaire des deux vecteurs de base.
La suite
E est un
On cherche des éléments de E de la forme
On résout l'équation
r=1 ou r=-2
P est un plan affine de
la forme générale des éléments de
i.e, un point plus une combinaison linéaire des deux vecteurs de base.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
