Intégration par changement de variables

[imp]

Bonjour.
Dans une intégrale telle que
I= |f(g(x))g'(x)=f(u)du avec g(x)=du , je n'arrive pas à comprendre comment déterminer u .
Pour prendre exemple mon cours, pour l'équation
I=x(arcsin(x^2))/√(1-x^4), on prend u=arcsin(x^2), afin de changer la variable, mais je n'arrive pas à comprendre comment trouver u.
Merci d'avance
( Le symbole | correspond au signe d'intégration)

[GaBuZoMeu]

Bonjour,

Quelques imprécisions qui rendent le discours flou. Par exemple, je ne vois pas d'équation, je vois une fonction dont on te demande de calculer une primitive.

As-tu calculé la dérivée de ?

Trouver un bon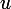 pour le changement de variable, c'est une affaire de flair, d'expérience et de tâtonnement. Il n'y a pas de recette miracle.

[mathelot]

bonsoir,
pour les intégrales des fonctions trigonométriques, il y a les règles de Bioche.
https://fr.wikipedia.org/wiki/R%C3%A8gles_de_Bioche

[imp]

Merci bien pour vos réponses, mais finalement, mon professeur m'a signalé que u nous sera donné dans chaque exercice.
Bonne soirée

[mathelot]

Dans une intégrale telle que
I= |f(g(x))g'(x)=f(u)du avec g(x)=du , je n'arrive pas...

les notations sont les suivantes:
u=g(x) (égalité entre fonctions)
du = g'(x)dx (égalité entre mesures)