Exercice de modèle de convergence

[Eagle2453]

Bonjour,
je me permets de demander de l’aide sur un exercice « taupinesque » dont j’ai la charge, si quelqu’un peut me guider, ça me serait d’une grande aide !
https://www.cjoint.com/doc/19_12/ILblEConWc7_07AF1206-0F88-4D30-B5C0-F257F2359EDC.jpeg

[LB2]

Bonjour,

tu peux raisonner avec des fonctions en escalier

[Eagle2453]

Ça j’y avais pensé, en construisant l'intégrale avec deux suites de fonctions en escalier qui encadrent l'intégrale, mais à partir de là, je manque d'idées j’avoue ...
Mon idée était surtout d’utiliser le théorème de Weirstrass pour tirer des conclusions

[tournesol]

As tu vu le théorème d'approximation de weierstrass qui dit que toute fonction continue sur un segment est limite uniforme de fonction polynomiales ?

[Eagle2453]

Oui je l’ai vu, c’est pour ça que j’y ai fortement pensé

[tournesol]

Alors c'est facile: puis
enfin toute fonction positive d'intégrale ...

[Eagle2453]

merci bien mais qu’est ce que f barre ici ?
Mon problème ici n’est pas tant de prouver pour une fonction continue, mais plutôt de le prouver ici pour une fonction continue par morceaux

[tournesol]

J'ai un peu de temps . Je vais t'aider . On oublie fbarre bien que ...réponse dans quelques minutes .

[tournesol]

On suppose f réelle et continue sur les intervalles et prolongeable sur tout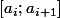
Soit e inférieur à
Soit qui coïncide avec f sur les intervalles ainsi que sur les pour i de 1 à n-1 , et qui est affine sur les intervalles pour i de 1 à n-1 .
Il existe une suite polynômes qui converge uniformément vers sur
et converge vers , intégrale qui est donc nulle .

Vrai pour tout e , etc.

[Eagle2453]

Bonsoir, merci tournesol ! La technique qui consiste à approcher les discontinuités par des morceaux d’affines est très utile ! Mais comment trouves tu ta dernière inégalité ? Tu utilises l’inégalité de la moyenne je suppose mais je ne vois pas trop sur quoi . Cependant, à la fin on trouve que l’intégrale de f au carré vaut 0, mais f n’étant pas continue, on ne peut pas utiliser la positivité améliorée ici, donc c’est pas évident de conclure ... encore merci pour ton aide !

[tournesol]

est nulle sauf sur n-1 intervalles de longueur 2e .
Les valeurs sont soit des valeurs de f , soit des valeurs intermédiaires entre des valeurs de f , ce qui explique que
Enfin la positivité de f^2 implique que
et aussi que et donc par continuité , fest nulle sur

[Eagle2453]

Merci tournesol ! Que Weirestrass vous bénisse !