Primitive (x^2+3)/(x^3+4x)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Guillaume1998
- Membre Naturel
- Messages: 42
- Enregistré le: 26 Fév 2019, 18:12
-
 par Guillaume1998 » 28 Nov 2019, 20:41
par Guillaume1998 » 28 Nov 2019, 20:41
Bonsoir,
Je suis bloqué sur cette primitive, si vous pouvez m'aider ?
dx)
Merci,
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 28 Nov 2019, 20:49
par Carpate » 28 Nov 2019, 20:49
Décomposition en éléments simples (voir théorie) :
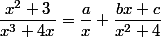
-
Guillaume1998
- Membre Naturel
- Messages: 42
- Enregistré le: 26 Fév 2019, 18:12
-
 par Guillaume1998 » 28 Nov 2019, 20:50
par Guillaume1998 » 28 Nov 2019, 20:50
Carpate a écrit:Décomposition en éléments simples (voir théorie) :
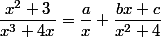
D'accord merci
-
Guillaume1998
- Membre Naturel
- Messages: 42
- Enregistré le: 26 Fév 2019, 18:12
-
 par Guillaume1998 » 28 Nov 2019, 21:03
par Guillaume1998 » 28 Nov 2019, 21:03
Carpate a écrit:Décomposition en éléments simples (voir théorie) :
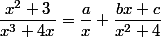
En fait je n'arrive pas à trouver car A=0 et pour trouver B et C il faut passer en nombre complexe d'apres la méthode que je viens de voir.
-
mathelot
 par mathelot » 28 Nov 2019, 21:14
par mathelot » 28 Nov 2019, 21:14
multiplier par x des deux côtés puis:
faire tendre x vers l'infini
puis
remplacer x par 0
ça donne a=3/4 et b=1/4
la fonction est impaire donc c=0
Modifié en dernier par mathelot le 28 Nov 2019, 21:17, modifié 1 fois.
-
Guillaume1998
- Membre Naturel
- Messages: 42
- Enregistré le: 26 Fév 2019, 18:12
-
 par Guillaume1998 » 28 Nov 2019, 21:17
par Guillaume1998 » 28 Nov 2019, 21:17
mathelot a écrit:multiplier par x des deux côtés puis:
faire tendre x vers l'infini
puis
remplacer x par 0
ça donne a=3/4 et b=1/4
Ok je viens de comprendre, merci beaucoup
-
mathelot
 par mathelot » 28 Nov 2019, 21:20
par mathelot » 28 Nov 2019, 21:20
la fonction est impaire donc c=0
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 29 Nov 2019, 09:36
par Carpate » 29 Nov 2019, 09:36
Ajout un peu tardif que Guillaume 1998 ne verra peut-être pas :
Dans un cas simple comme celui-ci, une réduction au même dénominateur du terme de droite suivie d'une identification des numérateurs respectifs
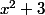
et
x^2+cx+4a)
donne
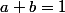
,
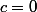
,
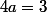
, etc ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités