Le carré disparu

[Budin]

Bonjour,
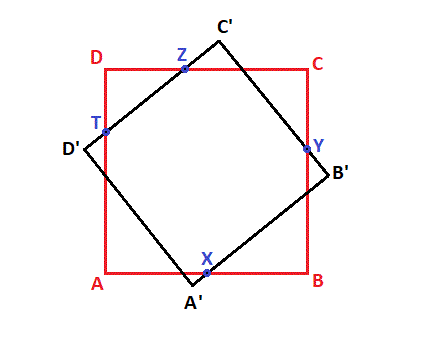
Il y a quatre points, X, Y, Z et T, chacun sur un des côtés (côtés-segments) d'un carré ABCD. Le carré est effacé, restent les points X, Y, Z et T. Il faut reconstruire le carré.

Cela ressemble au problème de Castillon, dont l'énoncé implique un triangle à reconstruire connaissant son cercle circonscrit et trois points qui sont sur les côtés (côtés-droites).

Je recherche une solution qui ne fasse pas massivement appel aux homographies.
J'ai fait quelques pas : le cercle de diamètre XY, par exemple, passe par un sommet du carré.
Si quelqu'un a une idée ou une piste , merci d'avance.

[Black Jack]

Salut,

Tu écris " Il faut reconstruire le carré."

L'article défini "le" suppose donc que ce carré est unique ...

Peut-être commencer par vérifier si c'est vrai par un petit dessin :



Voila 2 carrés de tailles différentes et respectant tous les 2 les conditions de l'énoncé.

Et donc ...

[Noemi]

Bonjour Budin,

Une piste avec les cercles, tu joins un point avec le centre des cercles et tu marques l'intersection de la droite avec le cercle. Tu obtiens ainsi 8 points qui te permettent de tracer deux carrés.

[tournesol]

Bonjour Black Jack
Tu n'as pas mis un point sur chacun des côtés .

[GaBuZoMeu]

C'est juste une étourderie de Black Jack, facile à réparer. À part cela, Black Jack a à la fois raison ... et tort.
Dans la situation qu'il décrit (points à l'intersection de côtés correspondants de 2 carrés), il y a en fait une infinité de carrés solutions : toutes les directions de côtés sont bonnes ! (Je m'affranchis de la contrainte que les points X,Y,... soient sur les côtés-segments, être sur les côtés-droites me suffit).



Mais ça, c'est un cas dégénéré. En général il y a bien un et un seul carré solution, facile à construire :



Légende : , , , . Les côtés passant par X et Z sont parallèles à w. Dans le cas dégénéré de Black Jack, w=0.

Je laisse la vérification du fait que la construction donne bien ce qu'on veut comme exercice.

[Black Jack]

Bonjour Black Jack
Tu n'as pas mis un point sur chacun des côtés .

Oui, distrait ...
Il suffit de descendre le point T de mon dessin pour le mettre à l'intersection de (AD) et (A'D') ...

[GaBuZoMeu]

Bon, le petit exercice n'intéresse personne, pas même le questionneur qui a semble-t-il oublié sa question.
Pas grave, c'était une question assez amusante.

[tournesol]

La vérif est triviale:
Avec A(0;0) , B(1;0) , C(1;1) , D(0;1) , X (a;0) , Y(1;b) , Z(c;1) et T(0;d) on obtient w(-a+b+c-d;0)
Ce qui est intéressant , c'est ton heuristique et en particulier pourquoi "rotationner" le vecteur v de pi/2 ?

[Budin]

pardon pour le délai. Il y a peu, quand une réponse arrivait, j'étais prévenu par email. Il semble que ce ne soit plus le cas. Merci à tous et en particulier à GaBuZoMeu, sa solution est très claire.
Amicalement,
JP

[GaBuZoMeu]

pourquoi "rotationner" le vecteur v de pi/2 ?

Un implicite qu'il convient d'expliciter : ABCD est parcouru dans le sens direct, X est sur (AB), Y sur (BC), Z sur (CD), T sur (DA).
Analyse : soit le vecteur unitaire de même direction et même sens que . Alors (la valeur commune est la longueur du côté du carré). Donc

Remarque : dans le cas dégénéré de Black Jack (plus d'une solution, donc une infinité) on a .

[tournesol]

Joli GaBuZoMeu , et merci .