Tracer une droite à partir des hauteurs

[Marmus1021]

Bonjour à tous !
J’ai un exercice sur les produits scalaires à faire, et je n’arrive pas bien la dernière question...
1- Soient A,B, C trois points du plan.
Établir que, pour tout point M du plan, on a MA.MB + MB.CA + MC.AB = vecteur nul
( tout en vecteurs bien sûr ).

Bon ça, c’est facile, j’ai juste décomposé les vecteurs et j’ai trouvé vecteur nul.

2- Déduire que les trois hauteurs d’un triangle non aplati sont concourantes.

Donc ça pareil, j’ai réussi en prenant un point M qui serait l’intersection de deux hauteurs. Le dernier produit scalaire serait nul aussi, donc M appartiendrait aux trois hauteurs.

3- Application : Deux droites d et d’ tracées sur une feuille de papier se coupent en un point P situé en dehors de cette feuille. A est un point de la feuille n’appartenant ni à d ni à d’. Tracer (AP) sans que les constructions ne sortent de la feuille.

Et la j’avoue que j’ai pas du tout réussi... Si quelqu’un trouve une solution, je suis preneur

[aymanemaysae]

Bonjour ;


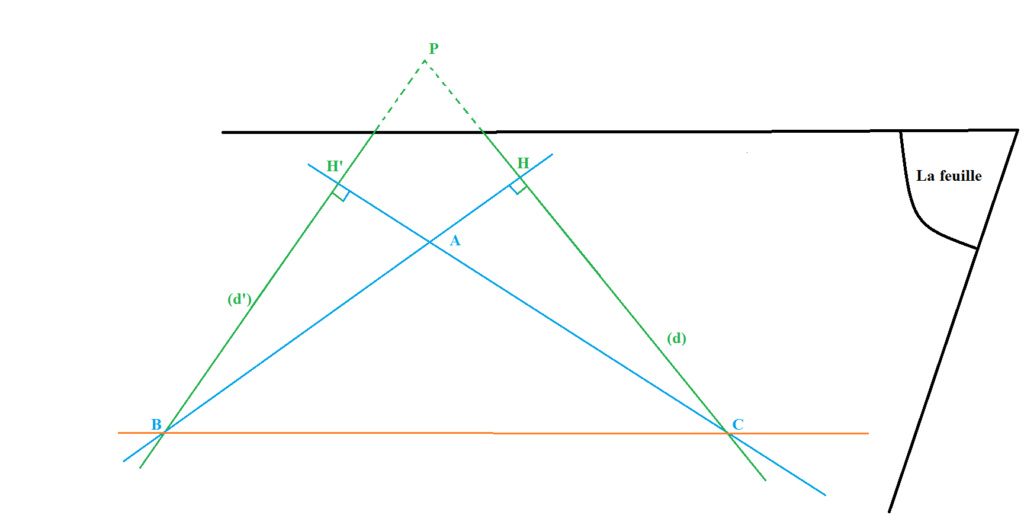
Soient H et H' respectivement la projection orthogonale de A sur la droite (d) et la projection
orthogonale de A sur (d') .

Soient B et C respectivement l'intersection de (AH) et (d') et l'intersection de (AH') et (d) .

En considérant le triangle ABC , tu as (CH) sa hauteur issue de C et (BH') sa hauteur issue de B .

Tu as maintenant tout ce qu'il faut pour conclure .

[aymanemaysae]

Bonjour ;

Voici une figure qui retrace ce que j'avais dit auparavant .