Bonjour à tous,
Je me permets de vous contacter car je ne comprends pas l'opération soulignée en rouge sur la photo ci-dessous.
https://www.casimages.com/i/191125111321224580.png.html
Pourquoi l'opération soulignée en rouge (1) devient (2) ?
Je me dis que (1) devrait s'annuler et être égal à 0. Par exemple, si (2b+1) = 4 et (2a+1) = 2, l'opération (1) reviendrait à faire 4x2 - 2x4 ce qui reviendrait à 0...
Quelqu'un pourrait m'expliquer la logique qui consiste à garder (2a+1) facteur de (2b+1) s'il vous plait ?
J'avais souligné également l'opération en vert car je ne comprenais pas pourquoi le +1 et le -1 s'annulaient mais je pense avoir compris. 2b+1 - 2a-1, - par mois ça fait + donc au final il s'agit de 2b+1 - 2a +1 donc annulation. Est-ce correct ?
Cordialement,
Incompréhension d'une opération
7 messages
- Page 1 sur 1
Re: Incompréhension d'une opération
Il s'agit de la réduction au même dénominateur de  (certainement pratiquée dès les petites classes du collège)
(certainement pratiquée dès les petites classes du collège)
Le dénominateur commun est le produit(2a+1)) car
car  et
et  n'ont aucun facteur commun.
n'ont aucun facteur commun.
Oui, =2a +1 -2b-1 =2(a-b))
C'est quand même le B A -BA du calcul algébrique !
Le dénominateur commun est le produit
Oui,
C'est quand même le B A -BA du calcul algébrique !
Re: Incompréhension d'une opération
Salut,
Tu racontes vraiment n'importe quoi.
On a f(a) - f(b) = 1/(2a+1) - 1/(2b+1)
Je reprends tes exemples, supposons : (2b+1) = 4 et (2a+1) = 2,
On aurait alors : f(a) - f(b) = 1/4 - 1/2
f(a) - f(b) = 1/4 - 2/4
f(a) - f(b) = -1/4 et certainement pas 0 comme tu le suggères.
************************************************
De manière générale :
1/A - 1/B (avec A et B différent de 0)
= B/(AB) - A/(AB) (mise au même dénominateur)
= (B-A)/(AB)
Donc : 1/A - 1/B = (B-A)/(AB)
************
Et en remplaçant A par (2a+1) et B par (2b+1), il vient :
1/(2a+1) - 1/(2b+1) = ((2b+1)-(2a+1))/((2a+1)(2b+1))
1/(2a+1) - 1/(2b+1) = (2b+1-2a-1)/((2a+1)(2b+1))
1/(2a+1) - 1/(2b+1) = (2b-2a)/((2a+1)(2b+1))
Qu'est ce que tu ne comprends pas là dedans ?

Tu racontes vraiment n'importe quoi.
On a f(a) - f(b) = 1/(2a+1) - 1/(2b+1)
Je reprends tes exemples, supposons : (2b+1) = 4 et (2a+1) = 2,
On aurait alors : f(a) - f(b) = 1/4 - 1/2
f(a) - f(b) = 1/4 - 2/4
f(a) - f(b) = -1/4 et certainement pas 0 comme tu le suggères.
************************************************
De manière générale :
1/A - 1/B (avec A et B différent de 0)
= B/(AB) - A/(AB) (mise au même dénominateur)
= (B-A)/(AB)
Donc : 1/A - 1/B = (B-A)/(AB)
************
Et en remplaçant A par (2a+1) et B par (2b+1), il vient :
1/(2a+1) - 1/(2b+1) = ((2b+1)-(2a+1))/((2a+1)(2b+1))
1/(2a+1) - 1/(2b+1) = (2b+1-2a-1)/((2a+1)(2b+1))
1/(2a+1) - 1/(2b+1) = (2b-2a)/((2a+1)(2b+1))
Qu'est ce que tu ne comprends pas là dedans ?
Re: Incompréhension d'une opération
Ce que je ne comprends pas ce sont les réponses pleine d'arrogance et de suffisance alors que je m'adresse poliment à vous.
Je pense m'être trompé de forum...
Je pense m'être trompé de forum...
Re: Incompréhension d'une opération
bonjour,
pour additionner deux quotients, on les "réduit au même dénominateur";ici, le dénominateur commun est leur produit (2a+1)(2b+1),on a le droit,sans changer la valeur d'un quotient,de multiplier numérateur et dénominateur par un même nombre, le 1er quotient est multiplié haut et bas par (2b+1) et le second quotient , haut et bas, par (2a+1). Une fois leur dénominateur étant commun, on ajoute les quotients en ajoutant leurs numérateurs,au dessus d'une même barre de fraction.Notons qu'une fonction est strictement décroissante sur un intervalle réel I , si et seulement si ses taux d'accroissement (f(a)-f(b))/(a-b) sont strictement négatifs, pour a et b quelconques appartenant à I.
pour additionner deux quotients, on les "réduit au même dénominateur";ici, le dénominateur commun est leur produit (2a+1)(2b+1),on a le droit,sans changer la valeur d'un quotient,de multiplier numérateur et dénominateur par un même nombre, le 1er quotient est multiplié haut et bas par (2b+1) et le second quotient , haut et bas, par (2a+1). Une fois leur dénominateur étant commun, on ajoute les quotients en ajoutant leurs numérateurs,au dessus d'une même barre de fraction.Notons qu'une fonction est strictement décroissante sur un intervalle réel I , si et seulement si ses taux d'accroissement (f(a)-f(b))/(a-b) sont strictement négatifs, pour a et b quelconques appartenant à I.
Re: Incompréhension d'une opération
Bonjour,
Merci pour votre réponse. Il s'agit effectivement d'une réduction au même dénominateur on ne peut plus classique dans le cas d'une addition/soustraction de fractions. Je ne sais pas pourquoi je suis allé me compliquer la vie comme ça...
Bref merci pour les explications.
Cordialement,
Merci pour votre réponse. Il s'agit effectivement d'une réduction au même dénominateur on ne peut plus classique dans le cas d'une addition/soustraction de fractions. Je ne sais pas pourquoi je suis allé me compliquer la vie comme ça...
Bref merci pour les explications.
Cordialement,
Re: Incompréhension d'une opération
Bonjour Sooon,
merci de ton message. Bien sûr qu'il faut savoir faire sans faute ces calculs algébriques.
Mais la technique employée par ton professeur est laborieuse.
De plus, il confond fonction croissante (les inégalités sont larges pour les antécédents et les images) avec fonction strictement croissante (inégalités strictes).
D'ailleurs la définition en rouge est incorrecte, il faut remplacer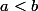 par
par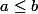
Il existe une meilleure technique.
Soit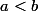
Alors , et les réels
, et les réels  et
et  sont strictement positifs.
sont strictement positifs.
Donc < 1/(2b+1)) car la fonction inverse x->1/x est strictement décroissante sur R+*.
car la fonction inverse x->1/x est strictement décroissante sur R+*.
La fonction inverse est une fonction usuelle donc j'utilise volontairement le résultat qu'elle est strictement décroissante sur R+*.
Si l'on veut le redémontrer, rien de plus simple : soit x,y >0 tels que x < y
Alors en divisant membre à membre par le nombre réel strictement positif xy, on a 1/x > 1/y
Donc la fonction inverse x->1/x est strictement décroissante sur R+*
L'idée générale de cette démonstration est qu'on peut utiliser la composition de fonction monotone pour montrer qu'une fonction est monotone. Tu n'as pas toujours besoin de calculer f(b)-f(a), ou de dériver une fonction (tu verras sans doute la dérivation plus tard)
merci de ton message. Bien sûr qu'il faut savoir faire sans faute ces calculs algébriques.
Mais la technique employée par ton professeur est laborieuse.
De plus, il confond fonction croissante (les inégalités sont larges pour les antécédents et les images) avec fonction strictement croissante (inégalités strictes).
D'ailleurs la définition en rouge est incorrecte, il faut remplacer
Il existe une meilleure technique.
Soit
Alors
Donc
La fonction inverse est une fonction usuelle donc j'utilise volontairement le résultat qu'elle est strictement décroissante sur R+*.
Si l'on veut le redémontrer, rien de plus simple : soit x,y >0 tels que x < y
Alors en divisant membre à membre par le nombre réel strictement positif xy, on a 1/x > 1/y
Donc la fonction inverse x->1/x est strictement décroissante sur R+*
L'idée générale de cette démonstration est qu'on peut utiliser la composition de fonction monotone pour montrer qu'une fonction est monotone. Tu n'as pas toujours besoin de calculer f(b)-f(a), ou de dériver une fonction (tu verras sans doute la dérivation plus tard)
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
