Primitive
14 messages
- Page 1 sur 1
Re: Primitive de sqrt(x^2-1)/x dx
Bonjour
Ca manque de précisions sur les intervalles où ça se passe.
Les primitives de) figurent en général dans la liste des primitives à connaitre.
figurent en général dans la liste des primitives à connaitre.
Ca manque de précisions sur les intervalles où ça se passe.
Les primitives de
Re: Primitive de sqrt(x^2-1)/x dx
arctan u correspond à la primitive de u'/(1+u²) et non 1/(1+u) car ici j'ai un fait un changement de variable !
Re: Primitive de sqrt(x^2-1)/x dx
Non, ici tu n'as pas "1/(1+u)" mais plutôt "du/(1+u^2)" ce qui correspond bien à arctan.
Re: Primitive de sqrt(x^2-1)/x dx
Yezu a écrit:Non, ici tu n'as pas "1/(1+u)" mais plutôt "du/(1+u^2)" ce qui correspond bien à arctan.
J'ai modifié ma question car ce n'était pas tres compréhensible
Re: Primitive de sqrt(x^2-1)/x dx
Et donc quand on intègre u'/(1+u^2) n'est-ce pas correct ?
Edit : je viens de voir ta modification, je te réponds sou peu, je n'ai pas vraiment lu le fil.
Edit : je viens de voir ta modification, je te réponds sou peu, je n'ai pas vraiment lu le fil.
Re: Primitive de sqrt(x^2-1)/x dx
en fait je comprends pas comment obtenir le + arctan(1/(sqrt(x²-1))) dans le résultat final
Re: Primitive de sqrt(x^2-1)/x dx
Yezu a écrit:Et donc quand on intègre u'/(1+u^2) n'est-ce pas correct ?
Edit : je viens de voir ta modification, je te réponds sou peu, je n'ai pas vraiment lu le fil.
ok merci
Re: Primitive de sqrt(x^2-1)/x dx
Je ne vois pas de problème étant donné que  est constant sur les intervalles où
est constant sur les intervalles où  ne s'annule pas!
ne s'annule pas!
Re: Primitive de sqrt(x^2-1)/x dx
Kolis a écrit:Je ne vois pas de problème étant donné queest constant sur les intervalles où
ne s'annule pas!
Tu penses que ma réponse est correcte ?
Re: Primitive de sqrt(x^2-1)/x dx
Rebonjour,
Ton corrigé utilise probablement l'identité
 = \pm\dfrac{\pi}{2}-\arctan(x)) où le
où le 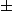 dépend du signe de
dépend du signe de 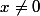 .
.
Ton corrigé utilise probablement l'identité
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
