vladi a écrit:ça se trouve c'est ça qu'il veut (je parie une mêche de cheveux de 30 cm de long et mes deux incisives inférieures)
Merci à viadi, mathelot et pascal 16 pour votre travail qui va m'aider à trouver la solution. Mais la période de 63 que vous indiquez me pose problème.
Donc je vous explique tout le problème ce sera plus simple (et plus compliqué sans doute!!!).
J'ai une sinusoide de 50 hertz soit une période de 20 millisecondes donnée par le courant domestique de "220V" qui sont en réalité 240V.
Sur une demi période soit 10 ms je veux avoir une augmentation de puissance linéaire donc cela fait intervenir aussi l'intensité du courant qui est une sinosoide on va dire synchrone avec la tension (pour un cos phi idéal de 1).
La question est combien de microsecondes en + pour augmenter la puissance (ou plutôt l'énergie) par paliers de 1/128ème.
L'équation que je vous ai donnée est celle qui résulte approximativement (graphiquement, les courbes se superposent) de mesures effectuées de la façon suivante:
Une résistance est alimentée pendant des valeurs de temps augmentant par 128ème de 10ms sur chaque 1/2 période. (Alimentation par angle de phase).
On mesure l'énergie utilisée en watts heure qui va de 0 à 2100.
En augmentant par paliers de 1/128ème de 10ms on a des valeurs d'énergie qui remplissent le tableau.
Je souhaite faire l'inverse : combien de microsecondes (ou de 128ème de 10ms cela me va aussi) pour une augmentation linéaire de l'énergie.
Pour éviter dans mon programme de faire appel à un tableau de 129 valeurs (de 0 à 128) je cherche l'équation qui le fait.
J'espère être clair et le problème sort du cadre mathématique pur.

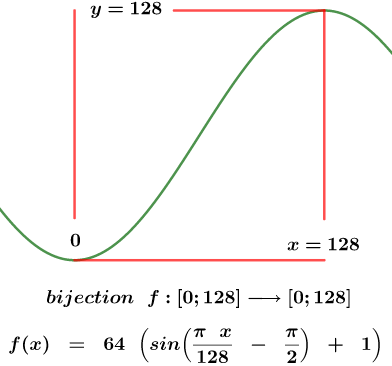

 ....
....