Calcul matriciel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ford9smith
- Membre Naturel
- Messages: 32
- Enregistré le: 10 Sep 2019, 00:10
-
 par Ford9smith » 20 Nov 2019, 18:24
par Ford9smith » 20 Nov 2019, 18:24
Bonjour,
Pourriez-vous m'aider à trouver où j'ai commis une erreur? Merci d'avance!
Soit la matrice

où a ∈ R.
Trouvez la matrice B telle que

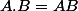
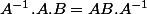
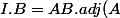. \frac{1}{Det (A)})
donc
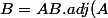. \frac{1}{Det (A)})
le déterminant de la matrice A = a² + 1
A est donc inversible.
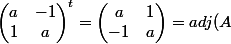)
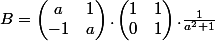
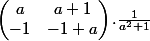
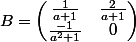
Pourtant, après vérification en multipliant la matrice A par la matrice B, je n'obtient pas la matrice AB.
Pourriez-vous m'indiquer où j'ai commis l'erreur?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 20 Nov 2019, 18:51
par GaBuZoMeu » 20 Nov 2019, 18:51
Tu t'es trompé dans l'ordre de la multiplication de matrice. Relis-toi.
-
Ford9smith
- Membre Naturel
- Messages: 32
- Enregistré le: 10 Sep 2019, 00:10
-
 par Ford9smith » 20 Nov 2019, 20:14
par Ford9smith » 20 Nov 2019, 20:14
GaBuZoMeu a écrit:Tu t'es trompé dans l'ordre de la multiplication de matrice. Relis-toi.
Donc
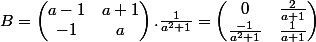
?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 20 Nov 2019, 21:10
par GaBuZoMeu » 20 Nov 2019, 21:10
Il est sérieux, ton deuxième signe = ?
Mais le problème vient dès le début :
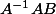
n'a aucune raison d'être égal à
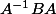
.
Ensuite, ta multiplication par le scalaire
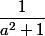
est aberrante.
Reprends tout ça.
Modifié en dernier par
GaBuZoMeu le 20 Nov 2019, 21:19, modifié 1 fois.
-
Ford9smith
- Membre Naturel
- Messages: 32
- Enregistré le: 10 Sep 2019, 00:10
-
 par Ford9smith » 20 Nov 2019, 21:17
par Ford9smith » 20 Nov 2019, 21:17
GaBuZoMeu a écrit:Il est sérieux, ton deuxième signe = ?
Oui
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 20 Nov 2019, 21:21
par GaBuZoMeu » 20 Nov 2019, 21:21
Tu plaisantes ?
Quand on multiplie une matrice par un scalaire, on multiplie tous les coeffcients par ce scalaire. Ton signe égal dit en particulier que quand tu multiplies
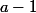
par
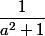
, tu trouves 0. Voila pourquoi je dis que tu plaisantes.
-
Ford9smith
- Membre Naturel
- Messages: 32
- Enregistré le: 10 Sep 2019, 00:10
-
 par Ford9smith » 20 Nov 2019, 21:30
par Ford9smith » 20 Nov 2019, 21:30
Ford9smith a écrit: GaBuZoMeu a écrit:Il est sérieux, ton deuxième signe = ?
Oui
Alors, A.B = AB
Si on ajoute la matrice inverse aux 2 membres, on obtient la matrice identité multipliée par B dans le 1er membre, ceci donne B = AB . A^(-1). Ce qui est très intéressant pour l'exercice.
La matrice inverse de A, A^(-1) = à la matrice adjointe adj (A) divisée par le déterminant de la matrice A.
Donc adj (A) / dét (A) = A^(-1).
Je ne comprends pas pourquoi ceci est aberrant pour vous.
En revanche, je serais ravi si vous pouviez me donner votre façon de faire.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 20 Nov 2019, 22:33
par GaBuZoMeu » 20 Nov 2019, 22:33
Mais non ! Tu continues à ne pas tenir compte de l'ordre de la multiplication !
De
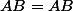
, en multipliant par
 à droite
à droite, tu obtiens ...
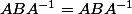
et certainement pas
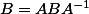
.
Pour le calcul de l'inverse,
}\,\mathrm{adj}(A))
ne me pose aucun problème. Ce qui est complètement aberrant, c'est la façon dont tu multiplies la matrice
)
par le scalaire
})
Comment te débrouilles tu pour faire ça ???
Peux-tu expliquer ?
-
Ford9smith
- Membre Naturel
- Messages: 32
- Enregistré le: 10 Sep 2019, 00:10
-
 par Ford9smith » 20 Nov 2019, 22:55
par Ford9smith » 20 Nov 2019, 22:55
GaBuZoMeu a écrit:Mais non ! Tu continues à ne pas tenir compte de l'ordre de la multiplication !
De
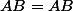
, en multipliant par
 à droite
à droite, tu obtiens ...
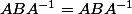
et certainement pas
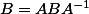
.
Pour le calcul de l'inverse,
}\,\mathrm{adj}(A))
ne me pose aucun problème. Ce qui est complètement aberrant, c'est la façon dont tu multiplies la matrice
)
par le scalaire
})
Comment te débrouilles tu pour faire ça ???
Peux-tu expliquer ?
Je vois... donc A^(-1) A B = A^(-1) AB
I B = A^(-1) AB
Pour la multiplication par le scalaire j ai fais n'importe quoi effectivement, je débute seulement dans le calcul matriciel.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 20 Nov 2019, 22:56
par GaBuZoMeu » 20 Nov 2019, 22:56
Bon, maintenant que tu as vu tes erreurs, tu peux reprendre sur de bonnes bases. Bon courage !
-
Ford9smith
- Membre Naturel
- Messages: 32
- Enregistré le: 10 Sep 2019, 00:10
-
 par Ford9smith » 20 Nov 2019, 22:59
par Ford9smith » 20 Nov 2019, 22:59
GaBuZoMeu a écrit:Bon, maintenant que tu as vu tes erreurs, tu peux reprendre sur de bonnes bases. Bon courage !
Merci beaucoup
-
Ford9smith
- Membre Naturel
- Messages: 32
- Enregistré le: 10 Sep 2019, 00:10
-
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
