Orthogonalité

[Koril]

Bonsoir,

Soit un s.e.v alors on a :

1) on a : si

2) supposons par l'absurde que
tel que .
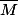
est compact et est un s.e.v fermé donc d’après le théorème d’ Hahn Banach géométrique, on a une séparation strict par une hyperplan fermé: et une forme linéaire f, ,
(1)
comme est un espace vectoriel alors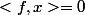

Je comprends pas cette dernière ligne. Est-ce que c'est dû au fait que si on prend une combinaison linaire de x, x dans , on a toujours avec et dans ?
d'où comme f est linaire on a: et si on fait tendre vers alors on a une limite infinie ce qui n'est pas possible avec l'inégalité du théorème (1)