Recherche primitive

[Guillaume1998]

-

[aymanemaysae]

Bonsoir ;


tu as : .

Une double décomposition en éléments simples fera l'affaire .

[Guillaume1998]

Bonsoir ;


tu as : .

Une double décomposition en éléments simples fera l'affaire .

Merci, par contre je ne vois pas ensuite comment faire car là premiere décomposition donne un A = 0 et B= 1/2

[Guillaume1998]

[Guillaume1998]

Bonsoir ;


tu as : .

Une double décomposition en éléments simples fera l'affaire .

Merci, par contre je ne vois pas ensuite comment faire car là premiere décomposition donne un A = 0 et B= 1/2

[fibonacci]

bonsoir;

décomposition:

[aymanemaysae]

Tu as : ;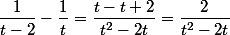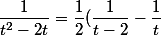

donc tu as : .

Tu as aussi : ;

donc : .

[Guillaume1998]

bonsoir;

décomposition:

Merci mais je ne vois toujours pas, on obtient encore le même résultat car le à et le b sont égaux à 0 et c=1/2

[aymanemaysae]

Je viens de compléter ma réponse d'en haut :

Tu as : ;

donc tu as : .

Tu as aussi : ;

donc : .

donc tu as : .

Tu peux conclure maintenant .

[fibonacci]

[Guillaume1998]

Je viens de compléter ma réponse d'en haut :

Tu as : ;

donc tu as : .

Tu as aussi : ;

donc : .

donc tu as : .

Tu peux conclure maintenant .

D’accord merci, mais je vois pas comment tu as trouvé cette décomposition ?

[Guillaume1998]

Je viens de compléter ma réponse d'en haut :

Tu as : ;

donc tu as : .

Tu as aussi : ;

donc : .

donc tu as : .

Tu peux conclure maintenant .

D’accord merci, mais je vois pas comment tu as trouvé cette décomposition ?

Comment tu as su qu’il fallait partir de la ?:

[aymanemaysae]

Quand on veut appliquer la décomposition en éléments simples à l'inverse d'un produit de deux facteurs p et q tels que p < q et q - p = a une constante non nulle , alors on calcule la différence 1/p - 1/q qui donne (q - p)/(pq)= a/(pq) ; donc on obtient : 1/(pq) = 1/a (1/p - 1/q) .

Pour 1/(t(t² - 2t)) , on a 1/(t(t² - 2t)) = 1/t x 1/(t² - 2t) = 1/t x 1/(t(t - 2)) .
On décompose en éléments simples tout d'abord 1/(t(t - 2)) qui donne 1/(t(t - 2) = 1/2 x (1/(t - 2) - 1/t) ;
donc on a : 1/(t(t² - 2t)) = 1/t x 1/2 x (1/(t - 2) - 1/t) = 1/2 x (1/(t(t - 2)) - 1/t²) .

On décompose aussi 1/(t(t - 2)) qui donne 1/2 x (1/(t - 2) - 1/t) ;
donc on a : 1/(t(² - 2t)) = 1/2 x (1/2 x (1/(t - 2) - 1/t) - 1/t²) = 1/4 x 1/(t - 2) - 1/4 x 1/t - 1/2 x 1/t² .

[Guillaume1998]

Quand on veut appliquer la décomposition en éléments simples à l'inverse d'un produit de deux facteurs p et q tels que p < q et q - p = a une constante non nulle , alors on calcule la différence 1/p - 1/q qui donne (q - p)/(pq)= a/(pq) ; donc on obtient : 1/(pq) = 1/a (1/p - 1/q) .

Pour 1/(t(t² - 2t)) , on a 1/(t(t² - 2t)) = 1/t x 1/(t² - 2t) = 1/t x 1/(t(t - 2)) .
On décompose en éléments simples tout d'abord 1/(t(t - 2)) qui donne 1/(t(t - 2) = 1/2 x (1/(t - 2) - 1/t) ;
donc on a : 1/(t(t² - 2t)) = 1/t x 1/2 x (1/(t - 2) - 1/t) = 1/2 x (1/(t(t - 2)) - 1/t²) .

On décompose aussi 1/(t(t - 2)) qui donne 1/2 x (1/(t - 2) - 1/t) ;
donc on a : 1/(t(² - 2t)) = 1/2 x (1/2 x (1/(t - 2) - 1/t) - 1/t²) = 1/4 x 1/(t - 2) - 1/4 x 1/t - 1/2 x 1/t² .

D’accord, merci beaucoup pour l’explication

[aymanemaysae]

Un chemin plus direct est le chemin donné au cours .



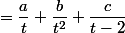avec a , b et c des nombre réels ;



;

donc on a : (- 2b = 1 et b - 2a = 0 et a + c = 0) <==> (b = - 1/2 et a = b/2 = - 1/4 et c = - a = 1/4 )

donc on a : .