Groupe A5

[Koril]

Bonsoir,

Pourquoi le produit d'un 3-cycle et d'un 5 cycle n'est pas dans A5?

[GaBuZoMeu]

Pourquoi écris-tu cela ? Un 3-cycle comme un 5-cycle sont des transformations paires (de signature 1), et donc leur produit l'est aussi.

[Koril]

Le but est de montrer que le groupe alterné A5 n'admet pas de sous-groupe d'ordre 15 en sachant que tout groupe d'ordre 15 est cyclique.

L'existence d'un sous-groupe d'ordre 15 dans A5 revient à l'existence d'un élément d'ordre 15 dans A5.
Tout élément de S5 peut s'écrire comme produit de cycles à support disjoint et tout cycle de longueur k est un élément d'ordre k. L'ordre d'un tel produit est le PPCM des ordres des cycles.

Un élément de A5 d'ordre 15 est (1) ou bien un un 15 cycles (On peut pas avoir un 15 cycles dans A5) (2) ou bien un le produit d'un 3-cycles par un 5-cycles à support disjoints.

Je n'arrive pas à saisir le (2)

Si et 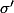sont deux permutations de longueur respective 3 et 5 alors

On obtient un permutation de signature 1.

[GaBuZoMeu]

C'est bien ce que je t'avais expliqué. Mais il y a une chose que tu as complètement oublié de mentionner, alors que c'est le principal : à supports disjoints.
Crois-tu qu'il existe deux parties disjointes ayant respectivement 5 et 3 éléments dans un ensemble à 5 éléments ?

[Koril]

Non ce n'est possible que dans un ensemble à 8 éléments. Donc on peut pas avoir un produit de 5-cycles et d'un 3-cyles à support disjoint dans A5, mais dans A8 oui.

[GaBuZoMeu]

Ben voila.