Produit scalaire

[Beta]

Bonjour,

J'ai une question, certainement un peu bête, en lien avec les produits scalaires,

Si on a pour tout ,



Avons nous et si oui pourriez vous le démontrer ?

En vous souhaitant une bonne fin de journée

Beta

[pascal16]

si E est de dimension finie, on prend comme famille de y les vecteurs d'une base.
ainsi tu as 2 vecteurs x et z avec toutes leurs coordonnées identiques

[GaBuZoMeu]

Je suppose que tu voulais demander :
Soient . Si pour tout on a , a-t-on ?
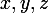
(La question telle que tu l'as posée avec quantification universelle sur n'a pas grand sens).

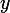
On peut réécrire l'égalité comme , et il suffit d'un seul (bien choisi) pour avoir la réponse.

[Beta]

Merci à vous deux pour vos explications !

Je suppose que l'on doit choisir y =0 car .
Or, est symétrique donc si ssi
Donc, .
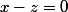
Ainsi, peut-on dire que car est vraie pour tout ? (cela me parait un peu léger, voir faux, mais je ne vois pas comment conclure autrement)

[GaBuZoMeu]

C'est faux, même très faux.

Quand est-ce que est nul ?

[Beta]

oulah,

En effet, mes précédents dire sont atrocement faux.

Donc, pour que il faut et il suffit que

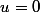
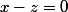
Ainsi, pour que il faut que et

D'où légalité entre x et z.

Est ce cela ?

[GaBuZoMeu]

Non, pas du tout.
Ton

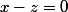
pour que il faut que et

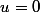
est encore atrocement faux, pour reprendre tes termes

Réfléchis !
Je t'ai donné l'indication que si et seulement si .
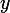
Ne vois-tu pas comment te servir de ce fait pour le choix d'un dans destiné à montrer que ?

[Beta]

y=0 ? autre que cela je ne vois pas

PS : Dans le précédent message, j'ai fais une faute de frappe qui est corrigé maintenant.

[GaBuZoMeu]

Ta correction ne change pas le fait que c'est une grosse erreur.

autre que cela je ne vois pas

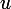
Là, tu vois mieux ? Il y a à la fois à gauche et à droite.

[Beta]

ah mais oui !
Pardon pour ma bêtise.


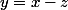
Merci GaBuZoMeu

[GaBuZoMeu]

Ben voila !