Probabilité

[Claraplp]

Bonjour,
J'aurais besoin d'aide pour résoudre un exercice, car je ne sais pas du tout comment m'en sortir. Voici l'énoncé :

Soit U et V deux variables aléatoires indépendantes suivant une loi uniforme sur [0,1] et X = U + V ; Y = U - V ; Z = U*V ; M = max(U,V) et N = min(U, V).

Donner les fonctions de répartition de X, Y, Z, M et N.

Merci d'avance

[GaBuZoMeu]

Dessine le carré 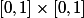représentant l'ensemble des valeurs que peut prendre le couple ( en abscisse, en ordonnée). Un événement concernant ces deux v.a. correspond à une partie de ce carré. Vu l'hypothèse d'uniformité et d'indépendance, la probabilité de l'événement est égale à l'aire de la partie correspondante (l'aire totale du carré est 1).
Il n'est pas difficile, par exemple, de trouver l'aire de la partie , en fonction de .

[Sylviel]

Si la visualisation géométrique de GaBuZoMeu ne te parle pas trop tu peut aussi commencer par max(U,V), à partir de la définition de la fonction de répartition, et de l'indépendance.

[Claraplp]

D'accord je pense avoir compris. Je vais essayer de résoudre cette exercice alors.
Merci beaucoup

[GaBuZoMeu]

Tu pourras donner les résultats que tu trouves.

[GaBuZoMeu]

Par exemple, la probabilité que est l'aire en bleu de la partie du carré unité sous la branche d'hyperbole . Le dessin est fait pour :



On peut se servir de ce calcul pour voir que l'espérance de est 1/4.

[Claraplp]

Merci pour vos indications, seulement je ne sais pas par ou commencer... je n'arrive pas à imaginer les étapes pour répondre à la question..

[GaBuZoMeu]

Qu'est-ce qui te pose problème ?
Le fait de comprendre que est l'aire que j'ai dessinée en bleu ?
Le calcul de cette aire ?

[Claraplp]

Le calcul en lui même car il y a plusieurs cas à différencier...
Je ne sais pas par où commencer

[GaBuZoMeu]

Tu as un rectangle de hauteur 1 au-dessus de l'intervalle . Je pense que tu peux calculer son aire.
Et il y a aussi l'aire sous la courbe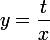 au dessus de l'intervalle . C'est un peu plus compliqué, mais puisque tu es dans le supérieur tu sais certainement calculer cette aire !

[Sylviel]

Sinon pour le maximum as-tu réussi ?

[Claraplp]

Merci pour toutes vos aides,
pour le maximum oui j'ai trouvé que la fonction de répartition était: 0 si t < 0; t² si 0<t<1 et 1 si t>1
pour X j'ai trouvé: 0 si t<= 0; t²/2 si 0<t<1; 1-(2-t)²/2 si 1<t<2 et 1 si t>= 2
pour Y j'ai: 0 si t<-1; (1+t)²/2 si -1<t<0; 1-(1+t)²/2 si 0<t<1 et 1 si t>1
pour Z j'ai; 0 si t<0; t-tlnt si 0<t<1 et 1 si t>1
pour N j'ai: 0 si t<= 0; 1-(1-t)² si 0<t<1 et 1 si t>1.

Est ce que c'est réponse vous semble correcte ?

[LB2]

Bonjour,

ton expression pour X se simplifie : les cas 0<t<1 et 1<t<2 (d'ailleurs, quid de t=1) sont confondus
C'est une loi triangulaire, cas particulier de la loi d'IrwinHall (obtenue en sommant n v.a. i.i.d de loi uniforme sur [0,1])

[GaBuZoMeu]

Oui, bravo Claraplp !

Je ne comprends pas trop la remarque de LB2 sur "les cas 0<t<1 et 1<t<2 sont confondus ".

Peux-tu déduire l'espérance de Z de ton calcul ?

[LB2]

C'était une bêtise, l'expression ne se simplifie pas plus