Probabilité montrer une espérance
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Laura0101
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Sep 2019, 20:53
-
par Laura0101 » 23 Oct 2019, 21:29
Bonjour,
j'ai un exercice à faire en probabilité mais je ne sais pas comment continuer, je sais qu'il faut utiliser l'indépendance pour réécrire l'espérance mais je n'arrive pas au résultat demandé, es-que quelqu'un aurait une piste pour m'aider?
Merci d'avance.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
par infernaleur » 24 Oct 2019, 00:11
Salut,
on a
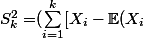])^2=$\sum_{i=1}^{k} [X_i-\mathbb{E}(X_i)]^2+2$\sum_{i<j}^{} [X_i-\mathbb{E}(X_i)][X_j-\mathbb{E}(X_j)])
Donc par indépendances des
)
tu as:
$)
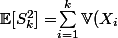Après tu as juste à utiliser la linéarité de l'espérance dans la formule de zéta et utiliser que
, ça fera apparaitres des sommes télescopiques.
-
Laura0101
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Sep 2019, 20:53
-
par Laura0101 » 05 Nov 2019, 20:52
Merci beaucoup j'ai réussi
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
