SUITES ET ALGORITHMES

[Hugo15]

Bonjour, cela fait plusieurs jours que je bloque sur des questions d'un devoir maison. Voici l'énoncé :

1. Algorithme pour trouver les "chiffres" de l'écriture en base b d'un entier.
Soit b un entier naturel (b supérieur ou égal à 2) fixé et x un entier naturel non nul. On considère la suite de division euclidienne suivante :
- de x par b : x b*q0+x0
- si q0 différent de 0, de q0 par b : q0 =
b*q1+x1
- :
- :
- si qk-1 différent de 0, de qk-1 = b*qk+xk etc

a. Montrer que la suite (qn) ainsi définie est strictement croissante.
b. En déduire que l'algorithme précédemment décrit finit par s'arrêter en donnant le quotient
qn = 0
c. Si n est le plus petit entier tel que qn = 0, montrer que :
x = xn*bn+xn-1*bn-1+...+
x1*b+x0
avec pour tout entier k, 0 inférieur ou égal à xk inférieur ou égal à b-1 et
xn différent de 0

d. Réciproquement, si (1) est réalisée, montrer que l'algorithme décrit au début de la question fournit comme restes les entiers (xk)
On dit que (1) est l'écriture de x en base b.

P.S. : Je ne suis pas dans le supérieur mais en terminale S.

[fatal_error]

hi,

qu'as tu fait

[Hugo15]

Pour être franc, je n'ai encore rien fait car je n'ai jamais fait ce genre d'exercice en classe et je n'ai aucune piste, ce n'est pas faute d'avoir cherché.

[fatal_error]

question 1 alors.
pour b=2,
pour x = 7
qu'obtiens tu pour q0, q1, ...

[Hugo15]

Pour b=2 et x=7, on obtient q0=3 et q1=1
C'est ça ?

[fatal_error]

x:7
q0 est tq x = q0*2+r0 (r0 < 2) donc q0 = 3 et r0 = 1
q1 est tq q0 = q1*2 + r1 donc q1 = 1 et r1 = 1
q2 est tq q1 = q2*2+r2 donc q2=0 et r2 = 1
donc on est ok.
conclusion numéro 1: la suite q(n) n'est pas croissante (et encore moins strictement croissante)

peux-tu montrer qu'elle est strictement décroissante?

[Hugo15]

Pour montrer qu'elle est décroissante, on peut simplement dire que qn diminue ?

[Hugo15]

x:7
q0 est tq x = q0*2+r0 (r0 < 2) donc q0 = 3 et r0 = 1
q1 est tq q0 = q1*2 + r1 donc q1 = 1 et r1 = 1
q2 est tq q1 = q2*2+r2 donc q2=0 et r2 = 1
donc on est ok.
conclusion numéro 1: la suite q(n) n'est pas croissante (et encore moins strictement croissante)

peux-tu montrer qu'elle est strictement décroissante?

Par contre je n'ai pas compris vos notations à gauche du signé égal à chaque ligne ? Et on est d'accord que t c'est b ?

[Hugo15]

Y'a-t-il quelqu'un pour m'aider svp ?

[fatal_error]

tq ca veut dire tel que (rien à avoir avec "b")

Pour montrer qu'elle est décroissante, on peut simplement dire que qn diminue ?

faut faire un peu plus d'effort que juste dire j'ai observé ça pour x=7 et b=2

pour tout k

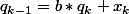
la div euclidienne dit que donc et b est entier positif, donc et il reste à gérer quand 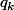vaut 0

[Hugo15]

Ah d'accord j'ai compris merci

[Hugo15]

Ensuite j'ai réussi toutes les autres questions sauf la d que je ne comprends pas

[fatal_error]

Ensuite j'ai réussi toutes les autres questions

nice :++:

pour la d,
de
pour , tu le trouves via
où

pour , tu peux réécrire
est tq

et grossomodo tu factorises à chaque fois le d'avant par b pour déduire
reste à être propre pour q_n

[Hugo15]

J'ai compris le principe mais en revanche ce que je n'ai pas compris, c'est en quoi cela nous aide à répondre à la question.