Peut on simplifier des soustraction d'exposant ?

[Boicamole]

Bonjour/bonsoir,
Je dois tout simplement de déterminer le sens de variation d'une suite Un = 4^(n+1)-4^n
je fais donc Un+1= 4^(n+2)-4^(n+1)

soit Un+1-Un = 4^(n+2)-4^(n+1)-( 4^(n+1)-4^n)
= 4^(n+2)-4^(n+1)-4^(n+1)+4^n
soit 4^(n+2)+4^n>-4^(n+1)-4^(n+1)
Un+1-Un > 0 Donc Un strictement croissant.

Pourriez vous me dire si ma démonstration est correcte

[fatal_error]

hello,

suspect:
quand tu arrives à = 4^(n+2)-4^(n+1)-4^(n+1)+4^n, OK
mais entre ton "soit" et ton "donc", c'est pas bon.
ton but c'est de montrer que 4^(n+2)-4^(n+1)-4^(n+1)+4^n > 0
La question est: a-t-on 4^(n+2)+4^n>-4^(n+1)-4^(n+1) ?
4^(n+2)+4^n>-4^(n+1)-4^(n+1) <=> 4^n( 16 + 1) > -4^n(4+4) <=> 17> -8 (car 4^n est positif)
et là effectivement tu dis: oui 17 est bien supérieur à -8 donc ...

[Boicamole]

hello,

suspect:
quand tu arrives à = 4^(n+2)-4^(n+1)-4^(n+1)+4^n, OK
mais entre ton "soit" et ton "donc", c'est pas bon.
ton but c'est de montrer que 4^(n+2)-4^(n+1)-4^(n+1)+4^n > 0
La question est: a-t-on 4^(n+2)+4^n>-4^(n+1)-4^(n+1) ?
4^(n+2)+4^n>-4^(n+1)-4^(n+1) <=> 4^n( 16 + 1) > -4^n(4+4) <=> 17> -8 (car 4^n est positif)
et là effectivement tu dis: oui 17 est bien supérieur à -8 donc ...

Oui je suis d'accord mais un chiffre ne prouve rien il faut démontrer avec n non ?

[fatal_error]

ben je sais pas trop avec quoi t'es d'accord.

Oui je suis d'accord mais un chiffre ne prouve rien il faut démontrer avec n non ?

mais on a fait pour tout n.
on a montré que l'expression u(n+1) - u(n) >= 0 est EQUIVALENTE à 17 >= -8 POUR TOUT n
quand à gauche c'est vrai, à droite c'est vrai et quand à droite c'est vrai, à gauche c'est vrai.
et à droite c'est TOUT LE TEMPS vrai, donc à gauche aussi.

si vraiment ça te gène, u(n+1) - u(n) = 4^(n+2)-4^(n+1)-4^(n+1)+4^n = 4^n(16 - 4 - 4 +1) = 4^n(9) et c'est positif...

edit: soit dit en passant, j'ai fait une erreur de signe en comparant 4^(n+2)+4^n> -4^(n+1)-4^(n+1), il fallait bien sûr comparer 4^(n+2)-4^(n+1)-4^(n+1)+4^n >= 0 <=> 4^(n+2)+4^n >= 4^(n+1)+4^(n+1)

[cassiopella]

Bonjour @Boicamole, avant de commencer la démonstration, je te conseille de factoriser l'expression de en simplifiant ainsi l'expression.

Pour rappel, ta suite est définie par : .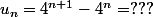

Une fois simplifié, la différence est facile à trouver.