Loi normale

[elodieb]

Bonjour,

Je bloque sur un sujet. J'ai deux loi normale de même esperance mais d'ecart type different.
X suit la loi N(50,2) et Y suit la loi N(50,5)
Je dois calculer la probabilité que X soit inferieur à Y
Pouvez vous m'aider?

[GaBuZoMeu]

Tes variables aléatoires sont indépendantes ?

, ça fait une belle symétrie !

Edit : correction faite pour bien avoir la symétrie par rapport à (50,50)

[LB2]

En fait, on n'a pas besoin de l'hypothèse que les v.a. soient indépendantes (car elles sont gaussiennes). Quelle est la loi de X-Y, par exemple ? l'idée est de se ramener à une proba que l'on sait calculer

[elodieb]

Elles sont indépendantes oui.
Je ne comprends pas ta réponse, peux tu m'expliquer ?
J'ai une autre question après mais avec des espérances différentes.
J'avais pensé à calculer la différence des deux fonctions de densité, ou les points d'intersection des deux courbes mais ca me parait compliqué. Les autres exercices que j'ai à rendre sont de simples applications.
Merci pour ton aide !

[elodieb]

X - Y ? Je ne sais pas.. je n'ai pas vu de cours la dessus, je suis un peu perdu

[Sylviel]

@LB2 je ne vois pas trop comment tu fais sans l'indépendance...

La combinaison linéaire de lois normales indépendantes est une normale, c'est un théorème fondamental que tu as probablement vu en cours.

Du coup il te suffit de déterminer espérance et variance de (X-Y) pour en déduire sa loi, puis la réponse à ta question

[GaBuZoMeu]

Mon histoire de symétrie ne te parle pas ?
J'explicite un peu :
Que fait la transformation sur la densité jointe ? Comment se comparent la probabilité que et celle que ?

[elodieb]

D'accord, donc je peux dire X - Y suit la loi normale d'espérance 0 et d'ecart type -3
X inferieure a Y equivaut à X - Y < 0
Ensuite je calcule P(X-Y) < 0, 1/2 me parait assez évident
Mon raisonnement est il juste ?

[GaBuZoMeu]

Un écart-type -3 ???

[LB2]

@Sylviel : mais oui bien sûr on a besoin de l'indépendance (penser à avec g affine tout bêtement), au temps pour moi.

@elodieb tu dois avoir dans ton cours un résultat qui énonce que si et sont normales indépendantes, alors 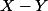suit une loi normale, d'espérance , et de variance , donc d'écart type ...

Ensuite, il est assez simple de finir la résolution en se ramenant à une loi normale centrée réduite,
quelles valeurs vas tu prendre pour et ?

Il faut faire bien attention si le deuxième paramètre des gaussiennes, dans la convention d'écriture de l'exercice, représente leur écart type ou leur variance.

Si tu n'a pas le droit d'utiliser ce résultat, on peut s'en passer avec la méthode de GaBuZoMeu, en raisonnant sur le vecteur gaussien (X,Y), dont tu dois connaitre la densité. Mais il faut calculer une intégrale double, qui n'est pas trop méchante normalement puisqu'ici le domaine d'intégration est assez simple modulo son astuce de symétrie.

Ici le problème est très simple car les espérances sont égales, mais la méthode fonctionne pour toutes valeurs d'espérance et de variance, tant que X et Y sont gaussiennes indépendantes.

[elodieb]

D'accord..
J'a du mal a comprendre la méthode de GabuZomeu..
J'ai donc 7 en écart type
Z = ((X-Y)-0)/7
P(Z<0) équivaut a P(X-Y)/7<0 equivaut a P(X-Y) <0 ?

[elodieb]

Donc je trouve 1/2 ?
En fait, peu importe l'écart type, tant que mes deux espérances sont égales, cela veut dire que j'aurai toujours 0,5 comme probabilité que X soit inférieur a Y ?

[beagle]

cela marche quelle que soit la distribution, loi (genre pas normale du tout!)? ayant une meme valeur du 50-50 de l'aire sous la courbe?

[LB2]

Donc je trouve 1/2 ?
En fait, peu importe l'écart type, tant que mes deux espérances sont égales, cela veut dire que j'aurai toujours 0,5 comme probabilité que X soit inférieur a Y ?

Ici, oui.

[LB2]

D'accord..
J'a du mal a comprendre la méthode de GabuZomeu..
J'ai donc 7 en écart type
Z = ((X-Y)-0)/7
P(Z<0) équivaut a P(X-Y)/7<0 equivaut a P(X-Y) <0 ?

Non, l'écart type de X-Y n'est pas 7 (on additionne les variances, pas les écart types)

[elodieb]

ah !
donc l'écart type est la racine de la variance,
la variance de X est donc 0.05², celle de Y, 0.07²
l'écart type de X - Y c'est la racine de (0.05²+0.07²), ce qui est environ égal à 0.086
est ce correct ?
Merci beaucoup de votre aide

[LB2]

cela marche quelle que soit la distribution, loi (genre pas normale du tout!)? ayant une meme valeur du 50-50 de l'aire sous la courbe?

Tant qu'on se ramène à une loi symétrique par rapport à sa moyenne et qu'on regarde la probabilité qu'elle dépasse (ou qu'elle soit en dessous) de sa moyenne, oui, il n'y a pas de raison.

A noter qu'ici on a utilisé que la somme de deux gaussiennes indépendantes reste gaussienne.
C'est une propriété de stabilité que possèdent d'autres "familles" de loi à paramètre (lois gammas, lois de poisson...)

[LB2]

ah !
donc l'écart type est la racine de la variance,
la variance de X est donc 0.05², celle de Y, 0.07²
l'écart type de X - Y c'est la racine de (0.05²+0.07²), ce qui est environ égal à 0.086
est ce correct ?
Merci beaucoup de votre aide

Je ne comprends pas pourquoi tout d'un coup 5 et 7 deviennent 0.05 et 0.07 ?
Sinon oui le raisonnement est correct
Encore une fois, sous réserve que dans ton exo, on note N(mu, sigma) avec sigma l'écart type et pas N(mu, sigma^2) ce qui se fait beaucoup aussi.

[elodieb]

ah oui pardon, c'est que j'ai plusieurs questions similaires avec des données différentes, et je m'emmêle les pinceaux
donc je pense avoir compris

merci beaucoup !!

[GaBuZoMeu]

Si tu n'a pas le droit d'utiliser ce résultat, on peut s'en passer avec la méthode de GaBuZoMeu, en raisonnant sur le vecteur gaussien (X,Y), dont tu dois connaitre la densité. Mais il faut calculer une intégrale double, qui n'est pas trop méchante normalement puisqu'ici le domaine d'intégration est assez simple modulo son astuce de symétrie.

Absolument pas, LB2. Il n'y a aucun calcul à faire !!!
Il y a juste à remarquer que la densité jointe est symétrique par rapport à (50,50).
Ceci suffit à établir que la probabilité de est égale à la probabilité de , qui elle-même est bien sûr égale à la probabilité de
Tout ce que ça utilise c'est que
et sont indépendantes,
ont même espérance
et ont toutes deux des distributions symétriques par rapport à l'espérance (p. ex. gaussiennes, uniformes etc.).