Polynomes prepa ece

[blanka]

Bonjour,
je suis en 1ère année de prépa ece je rencontre des difficultés sur 1 exercice pouvez vous m'aider svp

déterminer les polynômes unitaires vérifiant pour tout x appartenant à R ; P(x^2)=(x^3+1)*P(x)

merci beaucoup

[LB2]

Bonjour blanka,

tu peux raisonner par analyse synthèse.

Soit P solution. Que vaut nécessairement le degré de P ?
Donc sous quelle forme vas tu chercher P ?

[blanka]

merci pour ta reponse mais peut tu juste m'effectuer la démonstration histoire que je vois bien les étapes stp

[LB2]

l'idée c'est quand même que c'est toi qui cherches! tu peux répondre à mes questions intermédiaires?

[blanka]

le degré de p est égal à la somme des 2 autres degré

[blanka]

ce qui me gêne c'est que pX apparait 2 fois

[lyceen95]

Allons-y par tatonnement. Si P est de degré 1, est-ce que ça marche ? Idem, si P est de degré 2, ...
Puis plus sérieusement, si P est de degré n, quel est le degré du membre de gauche, et le degré du membre de droite ?
Je dis 'Plus sérieusement', mais la 1ère étape est indispensable.

[mathelot]

P(x^2) est un polynôme pair

[jsvdb]

Pour mémoire et avec égalité dans le cas .
Si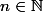 , et si désigne le polynôme défini par alors
Où la convention est d'attribuer le degré au polynôme nul et

[sofianmakhlouf]

Bonsoir
Si P est solution constante Alors P=0

Soit P une solution non constante. Notons d=deg(P)
On trouve 2d=3+d. Donc d=3

Donc il existe a,b,c,d dans IR tels que
P(X)=a X*3+b X*2+ c X+d
et tu remplace dans ton équation pour trouver a,b,c et d

[jsvdb]

Vu qu'on cherche des polynômes unitaires, on va plutôt poser .
Et bien entendu, on cherche des astuces pour éviter d'avoir à tout développer.

[tournesol]

d'après l'équation , les carrés des racines de 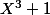sont racines de P .
Les racines de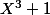 sont les racines cubiques de -1 , ie les pour k appartenant à {0;1;2}.
Leurs carrés sont les pour les mêmes trois k , ie les trois racines cubiques de l'unité .
Or P de degré 3 a au plus trois racines , et comme il est unitaire , .

[tournesol]

ERREUR sur le paramétrage des racines cubiques de -1
Ce sont les pour k appartenant à {0;1;2}
(produit de l'une d'entre elles par les racines cubiques de l'unité)
Leurs carrés sont les pour k appartenant à {0;1;2}
Or les pour k appartenant à {0;1;2} sont encore les trois racines cubiques de l'unité .

[mathelot]

autre démonstration qui ne demande pas de nombres complexes:

En changeant X en -X:

d'où (théorème de Gauss)
d'où car P est unitaire, de degré 3

[tournesol]

Magnifique mathelot !

[tournesol]

J'oubliais: magnifique aussi car ta démo est valable dans tout corps de caractéristique différente de 2 .

[tournesol]

mathelot , nous avons oublié la réciproque indispensable pour
D'autrepart , il pourrait être intéressant de déterminer les polynômes unitaires P tels que avec Q unitaire donné .

[mathelot]

Pour la réciproque,
le polynôme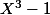 vérifie l'équation fonctionnelle (de même que le polynôme nul)