Application fondements mathematiques

par **GaBuZoMeu** » 22 Oct 2019, 10:11

Tu te mélanges complètement les pédales. Je fais un raisonnement complet pour la partition, et je sors.

Si

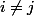
, on ne peut pas avoir à la fois

et

car ces deux égalités entraînent

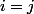
. Donc aucun

de

n'appartient à la fois à

et à

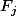
, ce qui veut dire que

et

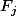
sont disjoints.
On a ainsi démontré que les

sont deux à deux disjoints.

Soit

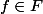
. Alors

par définition. Donc tout élément de

appartient à l'un des

, autrement dit la réunion des

est

tout entier.

Soit

. Alors la fonction constante

définie par

pour tout

appartient à

. Donc aucun des

n'est vide.

En conclusion,

est une partition de

.

par **Cyrils0303** » 22 Oct 2019, 10:18

J’ai pas tout compris.
Merci pour les réponses mais j’aimerai bien comprendre