Application fondements mathematiques

[Cyrils0303]

Soit n un entier naturel, avec n>=1. On note F l’ensemble des applications de [[1,n]] dans [[1,2n]].
1. Quel est le cardinal de F ?
2. Pour tout i apparentant à [[1,2n]], on note Fi={f appartenant à F/ f(1)=i}. Montrer que F1,F2,...,F2n forment une partition de F.
3 Montrer que l’on a card(F1)=card(F2)=...=card(Fn).
4. En utilisant les questions précédentes, déduire la valeur de card(F1).
5. Quel est le cardinal de l’ensemble G={f apparentant à F/ f(1)<=n} ?
On considère maintenant l’application
g:F->[[1,2n]]
f->f(1)
6. Montrer que g est surjective.
7. Montrer que g est injective si et seulement si n=1
Pouvez vous me venir en aide s’il vous plaît, je ne comprend rien du tout à cette exercice et j’aimerai bien le comprendre et le réussir ? Merci d’avance

[GaBuZoMeu]

Tu ne sais pas faire le 1 ? Compter le nombre d'applications d'un ensemble à n éléments dans un ensemble à 2n éléments ?
Pour le 2 : que faut-il montrer pour vérifier que est une partition de 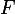? (Au besoin, revois dans ton cours la définition de partition).
Pour le 3 : le dernier n'est-il pas plutôt que ?

Courage, tu vas y arriver !

[Cyrils0303]

Pour la 1, comme il s’agit d’une application d’un ensemble à n élément dans un ensemble à 2n éléments, alors card(F)=(2n) à la puissance n
Pour la 2, il faut montrer que les ensembles F1,F2...,Fn sont des ensemble disjoint deux à deux
Pour la 3, j’ai vérifier, c’est bien card(Fn)

[GaBuZoMeu]

Pour la 1, comme il s’agit d’une application d’un ensemble à n élément dans un ensemble à 2n éléments, alors card(F)=(2n) à la puissance n

Tu vois, ce n'était pas difficile !

Pour la 2, il faut montrer que les ensembles F1,F2...,Fn sont des ensemble disjoint deux à deux

Ça va jusqu'à , et tu oublies quelque chose d'essentiel dans la définition de partition : revois la définition !

Pour la 3, j’ai vérifier, c’est bien card(Fn)

C'est qu'il y a une coquille dans l'énoncé. Ça va jusqu'à , c'est sûr !

[Cyrils0303]

une partition de l'ensemble F est une famille de toutes les parties non vides de F,disjointes deux à deux et dont la réunion est l'ensemble F.
Mais je comprends pas comment cette définition peut m'aider à résoudre cette question.
Pouvais vous juste m'expliquer le sens du début de la question s'il vous plait parce que l'intervention du i me pose probleme ?
pour la 3, puisque l'on aura dit dans la question 2 que F1,F2,...,F2n forment une partition de F, en revenant à la définition, on peut dire que l'on a card(F1)=card(F2)=...=card(F2n)
Mais on me demande de le montrer, donc je pense que cette explication n'est pas satisfaisante .

[GaBuZoMeu]

une partition de l'ensemble F est une famille de toutes les parties non vides de F,disjointes deux à deux et dont la réunion est l'ensemble F.
Mais je comprends pas comment cette définition peut m'aider à résoudre cette question.

Je dirais juste "une famille de parties non vides etc.", et pas "une famille de toutes les parties non vides etc.". Ça m'étonnerait que ce soit écrit comme ça dans ton cours.
Une définition sert à savoir précisément ce qu'il faut montrer. Il faut montrer
0° que les sont non vides
1° que les sont deux à deux disjoints
2° que leur réunion est .

Pouvez vous juste m'expliquer le sens du début de la question s'il vous plait parce que l'intervention du i me pose probleme ?

Quel problème cela te pose-t-il ? est un indice qui va de 1 à .

pour la 3, puisque l'on aura dit dans la question 2 que F1,F2,...,F2n forment une partition de F, en revenant à la définition, on peut dire que l'on a card(F1)=card(F2)=...=card(F2n)
Mais on me demande de le montrer, donc je pense que cette explication n'est pas satisfaisante .

Où vois-tu dans la définition d'une partition que toutes les parties de la partition ont même cardinal ? Dans une définition, il faut lire soigneusement tout ce qui est écrit, et rien d'autre que ce qui est écrit. Ne pas inventer autre chose.

[Cyrils0303]

d'accord, donc pour répondre à la question, il faut prouver ces trois points.
Je ne parviens pas à visualiser ce qu'il représente, sa façon d'agir dans l'énoncé.
Je me suis trompé en écrivant ce que je pensais et ce qui étais écrit dans l'énoncé.

[Cyrils0303]

En revanche je ne vois pas comment prouver ces trois points.

[GaBuZoMeu]

Prends un peu de temps pour réfléchir à ce qu'il faut montrer.

[Cyrils0303]

Il faut montrerque ces parties sont disjointes deux à deux et que la somme des cardinaux de ces parties forment l'ensemble F ?

[GaBuZoMeu]

Il faut montrer
que ces parties sont non vides
que leurs intersections deux à deux sont vides
que leur réunion est tout entier.
Attention à ce que tu écris : une somme de cardinaux, c'est un entier, ça ne peut pas être l'ensemble !

[Cyrils0303]

je ne vois pas comment démontrer ces trois points,
Pouvez vous m'aider s'il vous plait ?

[GaBuZoMeu]

Si 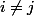, est il possible de trouver qui soit à la fois dans et dans ?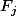
Souviens toi bien de ce que veux dire . Peux-tu rappeler ce que ça veut dire ?

[Cyrils0303]

Je suis pas sûr mais sa voudrais dire que l’element f est compris dans la partie Fi et donc par conséquent si i différent de j alors il n’y a pas d’element f qui se trouvent à la fois dans Fi et dans Fj. C’est très confus donc je suis pas sûr de ce que je vous met là

[GaBuZoMeu]

Tu ne réponds pas à ma question : que veut dire ?
Ce que je te demande n'est pas la mer à boire, c'est juste lire et comprendre la définition de :
est l'ensemble des applications de 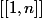dans telles que ?

[Cyrils0303]

Bas sa veut dire que l’element f appartient à la partie Fi
Et telles que je sais pas du tout, désolé c’est une matière que je comprends pas du tout

[GaBuZoMeu]

Comment lis-tu
?
Allez, je t'aide, je lis le début :
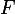" est l'ensemble des dans telles que .... "
Que mets-tu à la place des .... ?

[Cyrils0303]

Je dirai telle que f(1)=i

[GaBuZoMeu]

Ça serait mieux si tu en étais sûr ...

Est-ce qu'on peut avoir à la fois et si ?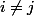
Traduction :
Est-ce qu'on peut avoir à la fois et si ?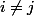
Conclusion ?

[Cyrils0303]

Fi et Fj sont deux parties différentes et doivent être disjointes deux à deux donc on peut pas avoir f(1)= i et f(1)=j si i différent de j
Donc conclusion, les parties Fi et Fj sont disjointes deux à deux