Bonjpurs,
je suis bloqué sur mon devoirs de maths. Voici l'énoncer :
U est la suite définie par U0= 0 et la relation de récurrence Un+1=((2Un)+3)/((Un)+4) pour tout entier n V est la suite définie pour tout entier n par Vn=((Un)-1)/((Un)+3)
1)Montrer que V est une suite géométrique dont on précisera le premier terme V0 et la raison.
Ce que j'ai fait c'est calculer V0 et la raison mais je ne sais pas comment démontrer que c'est une suite géométrique.
Merci.
Les Suites
12 messages
- Page 1 sur 1
Re: Les Suites
On calcule  fonction de
fonction de  ; ensuite on remplace dans l'expression
; ensuite on remplace dans l'expression  en fonction de
en fonction de 
On trouve alors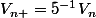
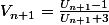
On trouve alors
Modifié en dernier par mathelot le 17 Oct 2019, 22:08, modifié 2 fois.
Re: Les Suites
marie2003 a écrit:Donc Vn+1 = (Un+1 -1)/(Un+1 +3) ?
oui.
Maintenant, remplace
formule de calcul
pour éviter les quotients de quotients
Re: Les Suites
marie2003 a écrit:Donc je remplace Un+1 par la formule que j'ai déjà?
oui, ça va donner
Re: Les Suites
oui ça me donne Vn+1 = (Un + 7)/(6Un + 19)
mais je ne vois toujours pas où vous voulez en venir
mais je ne vois toujours pas où vous voulez en venir

Re: Les Suites
marie2003 a écrit:oui ça me donne Vn+1 = (Un + 7)/(6Un + 19)
mais je ne vois toujours pas où vous voulez en venir
Calculs à revoir.
Tu devrais arriver à V(n+1) = (Un - 1)/(5Un + 15)
Détaille tes calculs pour voir où tu t'es trompé.
Re: Les Suites
@marie2003 : pour montrer que  est géométrique, le plan de calcul est le suivant :
est géométrique, le plan de calcul est le suivant :
1 - Exprimer en fonction de
en fonction de  (pas très difficile)
(pas très difficile)
2 - Dans cette expression, remplacer par une fonction de
par une fonction de 
3 - Exprimer en fonction de
en fonction de  (ça c'est plus compliqué, il faut inverser la relation donnant
(ça c'est plus compliqué, il faut inverser la relation donnant  en fonction de
en fonction de  )
)
4 - Simplifier tout cela et arriver à une relation de récurrence du type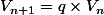
1 - Exprimer
2 - Dans cette expression, remplacer
3 - Exprimer
4 - Simplifier tout cela et arriver à une relation de récurrence du type
Re: Les Suites
titine a écrit:marie2003 a écrit:oui ça me donne Vn+1 = (Un + 7)/(6Un + 19)
mais je ne vois toujours pas où vous voulez en venir
Calculs à revoir.
Tu devrais arriver à V(n+1) = (Un - 1)/(5Un + 15)
Détaille tes calculs pour voir où tu t'es trompée.
Le 7 de
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
