Série de Fourier de f(x)=Ax^2+Bx+C
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
JCVD
- Messages: 8
- Enregistré le: 12 Oct 2019, 22:43
-
par JCVD » 17 Oct 2019, 01:59
Salut à tous!
Sauriez-vous trouver la série de fourier de f(x)=Ax^2+Bx+C de -Pi à Pi.
J'ai eu comme idée de calculer au préalable la série de fourier de f(x)=x^2+x. Est ce la bonne piste?
De plus, quelles sont les A, B et C pour que f soit continue sur le cercle ? Pour le coup je suis complètement perdue
Merci
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 17 Oct 2019, 06:45
va induire une fonction continue sur le cercle si et seulement si
=f(\pi))
.
-
jsvdb
- Membre Naturel
- Messages: 89
- Enregistré le: 20 Jan 2017, 09:45
-
par jsvdb » 17 Oct 2019, 10:09
Salut
Il me semble que la transformation de Fourier est linéaire, non :
 = A\mathcal F(x^2) + B\mathcal F(x)+\mathcal F(C))
Ici,
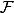
ne désigne pas tout-à-fait la transformée de Fourrier classique, mais l'application qui transforme f en sa série de Fourrier.
Bienheureux les fêlés car ils laissent passer la lumière !
-
sofianmakhlouf
- Membre Naturel
- Messages: 72
- Enregistré le: 03 Oct 2019, 15:54
-
par sofianmakhlouf » 17 Oct 2019, 16:10
Bonjours
Calculer les coefficients de Fourier en faisant deux intégrations par parties
-
JCVD
- Messages: 8
- Enregistré le: 12 Oct 2019, 22:43
-
par JCVD » 17 Oct 2019, 22:02
GaBuZoMeu a écrit: va induire une fonction continue sur le cercle si et seulement si
.
Alors quelles sont les valeurs pour A,B,C ? Je dois prendre des valeurs telles que f(-Pi_)=f(Pi) mais comment??
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 17 Oct 2019, 22:34
As-tu seulement écrit explicitement l'équation
 = f(\pi))
?
Qu'as-tu trouvé comme équation ? Conclusion ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
