équation

[pixies5]

bonjour tout le monde, j'aimerais savoir si des personne on compris un exo dont je n'ai rien compris merci beaucoup d'avance pour toute aide!

Exercice2

1.Factoriser x-4 à l'aide d'une identité remarquable.

2.En déduire une factorisation de A=(\sqrt{x}+2)(3sqrt{x}-8)+x-4.

3.Résoudre l'équation A=0

[pixies5]

les "\sqrt{x}" sont ; racine carré de x, car je n'arrive pas à les faire en toute forme.

[sofianmakhlouf]

bonjours
a*2-b*2=(a-b)(a+b)

[aymanemaysae]

Bonsoir;


1.


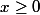
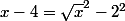
Pour tout ; tu as : ; puis avec le remarque de Sofianmakhlouf tu peux conclure .

Ps : Ceci après la remarque de M. Black Jack .

[mathou13]

Bonjour,

1.Factoriser x-4 à l'aide d'une identité remarquable.
(sqrtx-2)(sqrtx+2)
2.En déduire une factorisation de A=(\sqrt{x}+2)
(sqrtx+2)((3sqrt{x}-8)+(sqrtx-..)) en regroupant les sqrtx et les nombres du deuxièmes membres on pourra conclure.
3.Résoudre l'équation A=0
sqrtx=-2 impossible dans R
4sqrtx-...=0 <-> x=.... donc S={...}

[Black Jack]

Salut,

Ecrire : x-4 = (sqrtx - 2)(sqrtx + 2) sans rien d'autre n'est pas correct.

x-4 est défini pour tout x de R ... alors que (sqrtx - 2)(sqrtx + 2) n'est défini que pour x dans R+

[aymanemaysae]

Après la remarque de Black Jack que je salue bien , j'ai apporté les corrections nécessaires
à mon dernier post .