Classe d'équivalence

[Axelamour]

Salut à tous. Je bloque sur un exercice.
Pour chaque k€Z, Classe(k) désigne la classe d'équivalence de k pour la relation de congruence modulo n ( n€N).
Montrer que Cl(0), Cl(1),....., Cl(n-1) sont les seules classes d'équivalence. Autrement dit, montrer que {Cl(k) / k€Z} = { Cl(0), Cl(1),....., Cl(n-1) }.
Je procède par double inclusion. J'ai réussi a montrer l'inclusion inverse, mais je bloque sur l'inclusion directe. Comme indice, il faut utiliser la division écludienne. Aidez- moi svp. Merci!

[infernaleur]

Salut,
avec l'indication tu ne devrais pas avoir de mal normalement, tu peux écrire le début de ton raisonnement pour voir où est-ce que tu bloques.

[Axelamour]

J'ai commencé en disant que pour k € Z, l'ensemble des classes d'équivalence va de -i fini à + infini. Donc{Cl(0), Cl(1),....,Cl(n-1)} inclut dans {Cl(k)/k€Z}

[infernaleur]

L'inclusion que tu as montré est trivial, je te parlais de l'autre inclusion.
Tu commences donc par soit
Donc il existe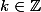 tels que
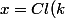Maintenant tu utilises ton indication et tu fais une division euclidienne (en se rappelant que ...)

[Axelamour]

Je n'arrive pas à comprendre. Peux-tu rédiger s'il te plaît ?

[sofianmakhlouf]

Soit x dans Z
Soit r le reste de la division euclidienne de x par n. On a 0=< r =< n-1
On a n divise x-r
donc cl(x)=cl(r)

[infernaleur]

Je n'arrive pas à comprendre. Peux-tu rédiger s'il te plaît ?

Tu peux écrire la division euclidienne de k par n, en précisant bien tout ce que tu écris ( c’est à dire où vivent toutes les variables que tu va écrire)

[Axelamour]

Mais pourquoi si n divise x-r, alors cl(x) = cl(r) ?

[GaBuZoMeu]

Peux-tu rappeler la définition de "x congru à y modulo n" ?

[Axelamour]

Ah oui je comprends. Comme n divise x-r , alors x est en relation avec r ce qui équivaut à dire que Cl(x) = cl(r). Merci