Fonctions polynômes

[RENE90]

Bonjour
J'ai un devoir à faire et je bloque déjà sur la 1ere question . Voici le début de l'énoncé :
Soit n appartenant à N tel que n supérieur ou égal à 2 . On considère la fonction polynôme f définie pour tout réel x par :
f (x) = x^n -1 + x^n-2 + ... + x^2 + x + 1
Démontrer que pour tout x appartenant à R on a x f(x) - f(x) = x^n - 1

Pourriez-vous m'aider svp ?

[pascal16]

aligne les mêmes puissances de x dans f(x) et xf(x), et tu vas comprendre le truc :
f (x) = ........ x^n -1 + x^n-2 + ... + x^2 + x + 1
xf(x)=x^n+x^n -1 + x^n-2 + ... + x^2 + x

[RENE90]

OK merci, bonne idée mais j'arrive à x^n + x - 1 et en factorisant : x(x^n - 1 - 1 ) - 1 et non pas au résultat demandé à savoir x^n - 1

[GaBuZoMeu]

OK merci, bonne idée mais j'arrive à x^n + x - 1

Regarde mieux !

[RENE90]

Bonjour GABuZoMeu
Rectificatif : Pour x f(x) - f(x) j'arrive à x^n - x^n-2 et toujours pas à x^n - 1

[Pisigma]

Bonjour,

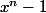
en partant de ce qu'a écrit pascal16

aligne les mêmes puissances de x dans f(x) et xf(x), et tu vas comprendre le truc :
f (x) = ........ x^n -1 + x^n-2 + ... + x^2 + x + 1
xf(x)=x^n+x^n -1 + x^n-2 + ... + x^2 + x

ben ça fait

[RENE90]

Eh oui ! Ce n'était pas très compliqué !
Merci à toi pour ton aide

[RENE90]

Dans cet exercice la deuxième question est :
"Pour tout x appartenant à R , isoler f(x) dans l'égalité précédente"

Je ne comprends pas très bien ce que l'on entend par "isoler" si ce n'est écrire f(x) = x f(x) - ( x^n - 1 ) mais en développant et réduisant cela , on va retomber sur l'expression de f(x) donnée dans l'énoncé

[lyceen95]

Non. Oublie la première question ... On part de x f(x) - f(x) = x^n - 1
Et il faut isoler f(x)

Quand tu écris f(x) = x f(x) - ( x^n - 1 ) , tu n'as pas isolé f(x), puisque f(x) apparaît à la fois à droite et à gauche du signe =.

[RENE90]

OK mais comment débuter pour parvenir à isoler f(x) ?

[GaBuZoMeu]

Il te faut écrire f(x)= qqchose où il n'y a pas de f
à partir de x f(x) - f(x) = x^n - 1

[RENE90]

Oui, mais quoi donc ?

[RENE90]

La seule chose que je pourrais faire, c'est soustraire les deux expressions définissant f(x) et xf(x) mais je vais retomber sur x^n - 1
A savoir :
f (x) = ........ x^n -1 + x^n-2 + ... + x^2 + x + 1
xf(x)=x^n+x^n -1 + x^n-2 + ... + x^2 + x

Alors quoi faire d'autre ?

[fatal_error]

quand t'as 5x+3x = 8x + 2, isoler x ca veut dire:
x(5+3-8)=2
x = 2/(5+3-8), là t'as x tout seul...

même chose si tu veux isoler f(x), si ca te gène appele le X... et isoles X

[aymanemaysae]

Bonjour ;


Je pense que tu dois étudier le cas où x = 1 et le cas où x 1 .

[lyceen95]

Pour que l'aide de Aynemasse te parle, on va te donner un autre indice.
Tu pars de
Cette égalité, tu peux aussi l'écrire :
Et là , les indices de Aynemasse ou fatal_error devrait t'aider à continuer.

[RENE90]

Oui, OK et j'en déduis donc que f(x) ) = (x^n - 1) / x - 1
Mais la question suivante de mon exercice est :
"En déduire, pour tout x appartenant à R \ {1} une factorisation de x^n - 1 et montrer que cette factorisation est valable pour tout réel x ( c'est à dire même pour x = 1 )"

Serait-ce :
x^n - 1 = (x - 1 ) (x^n-1 + x^n-2 + ... + x^2 + x + 1)

[lyceen95]

Bingo.

Si x est différent de 1, toutes les étapes du dessus montrent que cette égalité est vraie.
et si x = 1 alors on a 0 à gauche du signe égal et 0 également à gauche du signe =.

La factrisation est donc valable aussi pour x=1.

[Lostounet]

Bonjour
J'ai un devoir à faire et je bloque déjà sur la 1ere question . Voici le début de l'énoncé :
Soit n appartenant à N tel que n supérieur ou égal à 2 . On considère la fonction polynôme f définie pour tout réel x par :
f (x) = x^n -1 + x^n-2 + ... + x^2 + x + 1
Démontrer que pour tout x appartenant à R on a x f(x) - f(x) = x^n - 1

Pourriez-vous m'aider svp ?

f(x) est la somme de termes d'une suite géométrique de raison x (lorsque x différent de 1) et de premier terme 1:
f(x) = 1 + x + x^2 + ... + x^n

Donc f(x) = (1 - x^(n+1))/(1 - x)

Cela peut aussi s'écrire (1 - x)*f(x) = 1 - x^(n+1)
soit f(x) - x*f(x) = 1 - x^(n+1)

[RENE90]

Mon exercice n'est pas encore terminé, voici la question suivante :
" Soit a appartenant à R* et n appartenant à N tel que n supérieur ou égal à 2 . On considère la fonction g qui fait correspondre x à x^n - a^n définie sur R
a ) Pour tout x appartenant à R , factoriser g(x) par a^n
b ) Pour tout x appartenant à R , utiliser alors la formule vue précédemment ( il s'agit de f(x) = ( x^n - 1 ) / ( x - 1 ) ) pour factoriser g(x) , puis simplifier la factorisation obtenue en faisant apparaître le facteur x - a "