Déduire une fonction de sa représ graph

[SethGecko]

1)en remarquand que (C) est l'image, par une translation que l'on précisera, du graphique d'une fonction de référence, montrer que f est définie par : "f(x)=2x+7/2x+5"
la représentation graphique elle est du type "1/x" mai je voi pa comment démontré que "f(x)=2x+7/2x+5" car je trouve pas les translations qu'il fau faire

[SethGecko]

personne connait ?

[c pi]

Bonsoir

S'il s'agit bien de ,
on peut transformer cette expression comme suit (avec ) :
soit

En faisant le changement de variable et qui correspond bien à une translation, on met effectivement en évidence que cette expression est de la forme .

[annick]

Bonsoir,
on peut écrire y=(2x+7)/(2x+5)=(2x+5+2)/(2x+5)=(2x+5)/(2x+5) + 2/(2x+5)
y=1+2/(2x+5), soit y-1=2/(2x+5)
En posant Y=y-1 et X=2x+5, on obtient le changement de repère voulu, soit une translation de -5/2 i +j(i et j étant en vecteurs
Voilà, j'espère que cela t'aura éclairé. Je te souhaite bon courage pour continuer

[SethGecko]

je comprend tres bien la 1ere partie soie jusqua "y-1=2/(2x+5)" ou "y-1=1/(x+2,5)" mai ensuite jai du mal pour Y=y-1 et X=2x+5 je ne voie pas a quoi cela correspon

[c pi]

Tu vois bien que d'un point de vue formel,
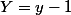on peut établir une relation entre et en posant que et .

Cela revient à dire que pour un point M de la courbe (C),

1° on peut considérer d'une part un repère
dans lequel M aura pour coordonnées telles que et ;

2° on peut considérer d'autre part un repère
dans lequel M aura pour coordonnées telles que et .

On passe d'un repère à l'autre par une translation de vecteur ou selon le sens considéré.

[SethGecko]

je ne comprend pa comment on passe de Y=2/x a la translation

[c pi]

je ne comprend pa comment on passe de Y=2/x a la translation

ATTENTION Ne mélangeons pas X et x, Y et y, 1 et 2...
sans quoi, en guise de translation, on n'aura qu'une inextricable confusion...

Je ne suis pas en mesure de t'expliquer comment "on passe de Y=2/x a la translation",
mais je peux tenter de reformuler le principe du changement de repère.

Entre les coordonnées (X,Y) liées au repère d'origine O' où la courbe (C) représente la fonction F telle que F(X)=1/X d'une part

et les coordonnées (x,y) liées au repère d'origine O où la même courbe (C) représente la fonction f telle que f(x)=(2x+7)/(2x+5) d'autre part

il y a une relation numérique qui s'exprime
- par X=x+2,5 (ou x=X-2,5) et qui se traduit graphiquement par un "décalage" de 2,5 unités parallèlement aux axes (Ox) et (O'X),
- par Y=y-1 (ou y=Y+1) et qui se traduit graphiquement par un "décalage" de 1 unité parallèlement aux axes (Oy) et (O'Y) ;

la résultante de ces deux "décalages" est un glissement rectiligne "oblique" selon une direction représentée par la droite (OO') sur une distance égale à OO' dans le sens de O vers O' (ou de O' vers O selon le sens considéré) ;
d'un point de vue mathématique, ce déplacement correspond à une transformation appelée translation.

Concrètement on pourrait illustrer la chose par la manipulation suivante :
- tracer sur une feuille de papier millimétré opaque
la courbe (C) représentant f(x) = (2x-7)/(2x-5) dans un repère d'origine O,
- tracer sur une feuille de papier calque millimétré un repère d'origine O' (avec des axes gradués et orientés identiquement au précédent),
- déplacer la seconde feuille sur la première de manière à placer O' au centre de symétrie de (C) et à ce que les axes (O'X) et (O'Y) soient les asymptotes de (C),
- choisir quelques points de (C) et lire leurs coordonnées dans chaque repère pour vérifier les relations entre X et x, Y et y indiquées plus haut.

[SethGecko]

a daccord jai enfin comprit merci a toi