Exercice
10 messages
- Page 1 sur 1
Re: Exercice urgent
Tu as eu quoi comme idée?
Et n peut-il valoir 0 ?
Et n peut-il valoir 0 ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Exercice urgent
Apres verification supposant que
2^(n+1)>n(n+1) et en montrant
2^(n+2)>(n+1)(n+2)
On a
2^(n+1)>n(n+1)
2^(n+2)>2n(n+1) la je suis bloque
2^(n+1)>n(n+1) et en montrant
2^(n+2)>(n+1)(n+2)
On a
2^(n+1)>n(n+1)
2^(n+2)>2n(n+1) la je suis bloque
Re: Exercice urgent
Bonjour
Il te suffit de remarquer que 2n est supérieur ou égal à n+2 pour n supérieur ou égal à 2.
Il te suffit de remarquer que 2n est supérieur ou égal à n+2 pour n supérieur ou égal à 2.
Re: Exercice urgent
Bonjour ;
Initialisation :
Pour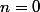 , on a :
, on a :  et
et =0) ; donc : 2^{n+1}>0(n+1) .
; donc : 2^{n+1}>0(n+1) .
Pour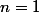 , on a :
, on a : 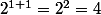 et
et =2) ; donc : 2^{n+1}>0(n+1) .
; donc : 2^{n+1}>0(n+1) .
Pour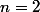 , on a :
, on a : 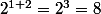 et
et =6) ; donc : 2^{n+1}>0(n+1) .
; donc : 2^{n+1}>0(n+1) .
Hérédité :
Soit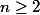 ; supposons qu'on a :
; supposons qu'on a : ) ;
;
donc :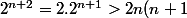 \ge (n+1)(n+2)) ;
;
car on a : .
.
Conclusion :) .
.
Initialisation :
Pour
Pour
Pour
Hérédité :
Soit
donc :
car on a :
Conclusion :
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
