Bonjour j'ai un dm de spé à rendre et j'ai 2 questions qui me posent problème.
1)Déterminer l'ensemble des entiers n tel que 2n+3 divise 3(n carré) +1 ?
le 3(n carré) m'embête je sais pas comment l'enlever
3) développer (x-5)(y-3) ?
j'ai trouver xy-3x-5y+15
Puis en déduire les couples d'entiers relatifs(x;y) solutions de l'équation : xy=3x+5y ?
Merci d'avance!
Entiers naturel n
9 messages
- Page 1 sur 1
Re: Entiers naturel n
Bonsoir
1) Suppose que 2n+3 divise 3n*2+1 et vois les conditions que tu obtiens sur n.
Indice: tu sais que si a/b et a/c alors a divise toute combinaison linéaire de b et c.
Or 2n+3/3n*2+1 et 2n+3/2n+3 donc avec une bonne combinaison linéaire tu peux annuler le 3n*2.
Puis tu refais cela jusqu'à avoir une condition simple. N'hésite pas à indiquer si cela est claire.
3)xy=3x+5y est équivalent à (xy-3x-5y+15)-15=0 soit (x-5)(y-3)=15 et alors ...
1) Suppose que 2n+3 divise 3n*2+1 et vois les conditions que tu obtiens sur n.
Indice: tu sais que si a/b et a/c alors a divise toute combinaison linéaire de b et c.
Or 2n+3/3n*2+1 et 2n+3/2n+3 donc avec une bonne combinaison linéaire tu peux annuler le 3n*2.
Puis tu refais cela jusqu'à avoir une condition simple. N'hésite pas à indiquer si cela est claire.
3)xy=3x+5y est équivalent à (xy-3x-5y+15)-15=0 soit (x-5)(y-3)=15 et alors ...
Re: Entiers naturel n
voila ce que j’ai trouver
2n+3/3n*2 +1 et 2n+3/2n+3
2(3n*2 +1) + (-3n) (2n+3)
6n*2 +2 -6n*2 -9n = -9n+2
2n+3/-9n+2 et 2n+3/-9n+2
2(-9n+2) + (9) (2n+3) = 30
est-ce correct pour l’instant ?
merci d’avance
2n+3/3n*2 +1 et 2n+3/2n+3
2(3n*2 +1) + (-3n) (2n+3)
6n*2 +2 -6n*2 -9n = -9n+2
2n+3/-9n+2 et 2n+3/-9n+2
2(-9n+2) + (9) (2n+3) = 30
est-ce correct pour l’instant ?
merci d’avance
Re: Entiers naturel n
Et pour la question 3
(x-5)(y-3) = 15
x-5=15 donc x=10
y-3=15 donc y=12
c’est correct ?
(x-5)(y-3) = 15
x-5=15 donc x=10
y-3=15 donc y=12
c’est correct ?
Re: Entiers naturel n
slt,
pour ta question de 07:12, vu que t'as rien parenthèsé concernant tes divisions, ta première ligne est déjà fausse
pour la question 3 c'est faux aussi. t'as qu'à remplacer tes résultats dans (x-5)(y-3) pour vérifier si ca fait 15.
(x-5)(y-3)=15 doit te faire dire: quels sont les diviseurs de 15: 1,3,5,15
tu regardes alors (x-5) lorsqu'il prend la valeur de chacun de ces diviseurs (et tu déduis le y associé)
ex:
si x-5==1, alors y-3==15
x = 6 et y=18
pour ta question de 07:12, vu que t'as rien parenthèsé concernant tes divisions, ta première ligne est déjà fausse
pour la question 3 c'est faux aussi. t'as qu'à remplacer tes résultats dans (x-5)(y-3) pour vérifier si ca fait 15.
(x-5)(y-3)=15 doit te faire dire: quels sont les diviseurs de 15: 1,3,5,15
tu regardes alors (x-5) lorsqu'il prend la valeur de chacun de ces diviseurs (et tu déduis le y associé)
ex:
si x-5==1, alors y-3==15
x = 6 et y=18
la vie est une fête 
Re: Entiers naturel n
J’ai bien compris pour la question 3!
mais je suis toujours bloque sur la question 1 ? merci d’avance
mais je suis toujours bloque sur la question 1 ? merci d’avance
Re: Entiers naturel n
Bonjour ;
Pour la question n° 1 , voici une méthode parmi d'autres .
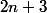 divise
divise 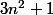 si il existe k un nombre entier naturel non nul tel que :
si il existe k un nombre entier naturel non nul tel que :  ;
;
donc :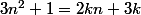 ; donc :
; donc :  = 0) ; donc :
; donc : 
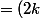^2 + 2 . 9 . (2k) + 9^2 - 81-12 = (2k+9)^2 - 93) .
.
Une condition pour que = 0) ait des solutions appartenant à
ait des solutions appartenant à  est
est
que soit un carré parfait ; donc on doit nécessairement avoir :
soit un carré parfait ; donc on doit nécessairement avoir : 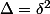 avec
avec  .
.
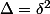 ; donc :
; donc : ^2-93=\delta^2) ; donc :
; donc : ^2-\delta^2=93) ;
;
donc :(2k+9+\delta)=93=1\times93=3\times31) .
.
Je crois que tu peux terminer tout seul cet exercice .
Pour la question n° 1 , voici une méthode parmi d'autres .
donc :
Une condition pour que
que
donc :
Je crois que tu peux terminer tout seul cet exercice .
Re: Entiers naturel n
Bonjour
mcfit dans ton second message une petite erreur de calcul c'est 31 et non 30. Donc tu obtiens (2n+3)/31 ce qui restreint fortement les valeurs de n possibles. Ensuite il suffit de voir parmi celles qui restent celles qui fonctionnent.
La solution de aymanemayse te permet de ne pas avoir de nombreux cas à vérifier à la fin.
mcfit dans ton second message une petite erreur de calcul c'est 31 et non 30. Donc tu obtiens (2n+3)/31 ce qui restreint fortement les valeurs de n possibles. Ensuite il suffit de voir parmi celles qui restent celles qui fonctionnent.
La solution de aymanemayse te permet de ne pas avoir de nombreux cas à vérifier à la fin.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
