slt,
j'ai une méthode pas très élégante parce que calculatoire mais bon...
on peut calculer les deux sommes... et constater qu'elles valent pareil.
je commence par la plus simple
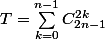
on peut étudier la série génératrice
 = \sum_k a_k x^k)
et remarquer que
 + A(-x) = \sum_k a_k X^k(1+(-1)^k))
et en particulier, quand k est pair, on a

et 0 pour k impair.
idem
 + A(-x)}{2} = \sum_k a_{2k} X^{2k})
pour X = 1, on a alors
 + A(-1)}{2} = \sum_k a_{2k})
et si on pose
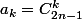
et qu'on somme jusqu'à 2n-1, on a alors via le binome de newton
 = 2^{2n-1})
 = 0)
et on déduit
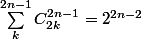
maintenant pour
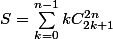
on veut cette fois faire disparaitre les termes pairs.
on remarque que (1): pour
 = x \sum_k a_kX^k)
on a
 - B(-x) = \sum_k a_k X^{k+1}(1+(-1)^{k+1}))
et du coup même chose mais on garde les termes de k impair
 - B(-x) = \sum_k a_{2k+1} X^{2k+2}(1+(-1)^{2k+2}))
ensuite, si tu dérives par rapport à X, tu fais apparaitre k+1...que je coupe en k et 1
(2):
 - B'(-x) = 2\sum_k ka_{2k+1} X^{2k+1}(1+(-1)^{2k+2}) + 2\sum_k a_{2k+1} X^{2k+1}(1+(-1)^{2k+2}))
En posant (depuis (1))
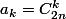
il vient
 = x(1+x)^{2n})
, que tu sais dériver
Enfin, (2) évalué en
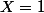
,
 - B'(-1)}{2} = S + \sum_k a_{2k+1} X^{2k+1})

ne devrait plus te poser de problème
puis tu déduis S

