Polynome du second degré 1ere

[Ca1y]

Bonsoir,
J'ai un DM de Mathématiques à rendre lundi, cela fait 2 jours que j'essaie d'y répondre mais en vain.
J'ai essayé plusieurs calculs pour la deuxième question, mais les résultats ne sont pas les mêmes que sur la feuille.
Je vous prie de m'aider, merci d'avance.


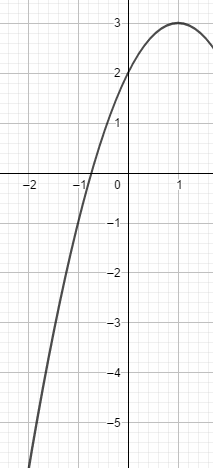
On considère la fonction polynôme du second degré f dont on donne la représentation graphique Cf ci- dessous. on note A,B,C et D les points de la courbe d'abscisses respectives -2, -1, 0 et 1.

Dans cet exercice les parties A et B sont indépendindépendantes.

PARTIE A:
1. Déterminer graphiquement f(-2);
f(-1); f(0) et f(1).
2. On note g la fonction définie sur R
par g(x) = f(x-1) et Cg sa courbe représentative.
Justifier que g(-1) = -6 puis calculer g(0); g(1) et g(2).
3. Placer dans le repère les points A', B',
C'et D' d'abscisses respectives -1 ; 0 ; 1 et 2.
4. Quelle transformation du plan
associe A à A', B à B', C à C' et D à
D' ? on demande de préciser son(ses)
élément(s) caractéristique(s).
5. En déduire une méthode pour tracer
la courbe Cg à partir de Cf

PARTIE B:
1. Déterminer graphiquement les
coordonnées dụ sommet de la
parabole.
2. En déduire la forme canonique de la
fonction f.
Donner la forme développée de la
fonction f.
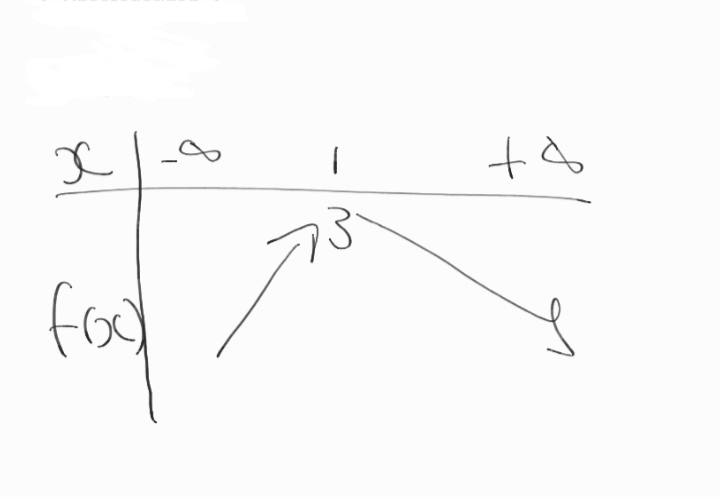
4. Dresser le tableau des variations de
f.

[Ca1y]

PARTIE A:
1. f(-2) = -5,8
f(-1) = -1
f(0) = 2
f(1) = 3

2. g(x) = f(x-1) : sa courbe représentative est donc la même que celle de la fonction f mais avec -1 d'abscisse par rapport à elle.

Justifier que g(-1) = -6 :
J'ai essayé de trouver f(x) pour trouver g(x)
La courbe est une parabole avec a<0 donc a est négatif.
(J'ai suivi les instructions de cette vidéo pour la suite https://youtu.be/F4t6y-jRJEc)
D'après une lecture graphique, on a les racines (qui passent par 0) u=-0.8 et v=2.7
Puisqu'on connait les deux racines on utilise la forme factorisée:
f(x) = a(x-u)(x-v)
f(x) = a(x+0.8)(x-2.7)
D'après le graphique x=0 quand y=2
Donc pour trouver a:
f(0) = a(0+0.8)(0-2.7)
f(0) = a(0.8*(-2.7))
f(0) = -2.16a
Mais f(0)=2 donc
-2.16a = 2
a = 2/(-2.16)

f(x) = 2/(-2.16) (x+0.8)(x-2.7)

Donc g(x) = 2/(-2.16) ((x-1)+0.8)((x-1)-2.7)
Justifier que g(-1) = -6
g(-1) = 2/(-2.16) ((-1-1)+0.8)((-1-1)-2.7)
g(-1) = 2/(-2.16) (-2+0.8)(-2-2.7)
g(-1) = 2/(-2.16) (-1.2)(-4.7)
g(-1) ≃ -5.22

[Ca1y]

Je n'ai jamais appris à déterminer une fonction à l'aide d'une simple parabole, je pense que la réponse n'est pas la bonne. S'il y a une façon plus simple/compréhensible je suis preneuse.

Pour la partie B j'ai fait :
PARTIE B:
1. S(1;3)
2. En déduire la forme canonique de la
fonction f.
f(x) = a(x-α)+β
f(x) = a(x-1)+3
(Parce que x correspond à α et y à β ?)

4.

[vladi]

On considère la fonction polynôme du second degré f dont on donne la représentation graphique Cf ci- dessous.

bonjour

l'image n'apparait pas

ça serait pas ça des fois?



(j'en suis certain)

[lyceen95]

Partie A)
Je fais confiance au dessin de vladi (et je crois qu'on peut lui faire confiance).
Du coup, la 1ère réponse f(-1) = -5.8 est fausse.

Et même si vladi s'est planté, j'ai 100 000 raisons de penser que ce -5.8 est faux.

[GaBuZoMeu]

C'est f(-2) qui d'après Ca1y vaudrait -5.8.
La lecture sur le graphique n'est pas tout à fait bonne. Et le dessin de vladi ne descend pas assez bas.

[vladi]

Et le dessin de vladi ne descend pas assez bas.

c'est fait exprès
la fonction est du second degré et sa dérivée s'annule en valeur d'abscisse 1

on a cinq points de la parabole pour trois inconnues a,b,c de

(-1,f(-1))
(0,f(0))
(1,f(1))
(2,f(2))
(3,f(3))

[lyceen95]

Ca1y nous dit qu'on a une parabole qui passe par ces 4 points : f(-2) = -5,8
f(-1) = -1
f(0) = 2
f(1) = 3

Or, je ne vous apprends rien, il n'y a pas de fonction de la forme f(x) = ax²+bx+c qui passe par ces 4 points.
En plus, quand on est au lycée, les profs sont sympas, ils donnent des exercices avec des nombres simples, des nombres entiers par exemple.
Donc, puisqu'il faut éliminer au moins une des 4 mesures de Ca1y, j'élimine la mesure f(-2)=-5.8 .
Et bonne nouvelle, si je la remplace par f(-2)=-6, alors il y a bien une fonction f(x)=ax²+bx+c qui convient.

[Ca1y]

J'ai peut-être fait une erreur pour f(-2) = -5.8 alors, même si c'est ce que je lis sur le graphique, je vais faire confiance à lyceen95 et dire que f(-2) = -6.

Voici la photo
https://i.postimg.cc/Y94nGcKh/20190920-225510.jpg

[vladi]

même si c'est ce que je lis sur le graphique, je vais faire confiance à lyceen95 et dire que f(-2) = -6.

c'est un problème de vue car même sur ton graphique on voit bien que f(-2)=-6

[Ca1y]

Donc,
f(-2) = -6
f(-1) = -1
f(0) = 2
f(1) = 3

Mais comment trouver la fonction f(x) = ax^2+bx+c ?

[vladi]

Donc,
f(-2) = -6
f(-1) = -1
f(0) = 2
f(1) = 3

Mais comment trouver la fonction f(x) = ax^2+bx+c ?

en seconde tu as vu que est une fonction paire

donc à la limite si tu sais que la dérivée s'annule en 1 et que tu connais f(1)

et que tu connais f(-1) et f(0) alors tu connais f(2) et f(3)

mais tu n'a pas besoin de les connaître f(2) et f(3) tout comme tu n'as pas besoin de connaître f(-2)

et en plus tu n'as pas besoin de connaître f(-1)

regarde ton cours en seconde
On doit tout te dire????


pour trouver les coefficients du polynôme

est la dérivée

et tu sais que

donc



donc c=2



donc ....
[Message effacé sur la demande du posteur]

[lyceen95]

La plus grande difficulté dans cet exercice, c'est qu'il faut sortir du cadre habituel. Dans 98% des exercices, on nous demande de trouver . Là, on a un qui se promène; mais on ne nous demande pas de trouver . On nous demande de trouver .
C'est ça la plus grosse difficulté.