Etude d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nanos
- Messages: 9
- Enregistré le: 14 Sep 2019, 10:37
-
 par Nanos » 14 Sep 2019, 10:44
par Nanos » 14 Sep 2019, 10:44
Bonjour à tous, je suis nouveau sur ce forum, j'espère que cela se passera bien.
Je bloque sur un exercice qui semble vraiment classique, ce qui me fruste énormément.
Soit u = (un) une suite bornée de nombres réels telle que

Montrer que lim un = 0.
J'ai tenté d'exploiter le fait que la limite au dessus était égale à 0 par la définition usant les Epsilons, le fait que un est bornée mais rien n'y fait. J'indique aussi que je me suis un peu fixé l'idée de démontrer la convergence vers 0 de un par la limsup et la liminf, et donc montrer que 0 >= limsup(un) et liminf(un) >= 0 (je ne sais pas si c'est la meilleure approche, mais en général ça semble bien marcher).
Auriez-vous une piste sur laquelle m'aiguiller ? Je ne demande en aucun cas la réponse bien entendu

Merci.
-
rog974
- Messages: 8
- Enregistré le: 11 Mar 2015, 19:05
-
 par rog974 » 14 Sep 2019, 11:09
par rog974 » 14 Sep 2019, 11:09
Bonjour.
On peut montrer que la suite
)
admet au moins une valeur d'adhérence (d'après ...). Comme la limite

, on peut avoir une idée des (ou de la...) valeur(s) d'adhérence.
Ainsi, la suite
)
est bornée et admet une unique valeur d'adhérence, elle est donc...
Voilà pour un début...
-
Nanos
- Messages: 9
- Enregistré le: 14 Sep 2019, 10:37
-
 par Nanos » 14 Sep 2019, 11:10
par Nanos » 14 Sep 2019, 11:10
Oh très bien, je vais explorer cette piste, je reviens vers vous si j'ai d'autres questions ou si je n'ai pas réussi.
Merci beaucoup, et bonne journée.
-
Nanos
- Messages: 9
- Enregistré le: 14 Sep 2019, 10:37
-
 par Nanos » 14 Sep 2019, 11:41
par Nanos » 14 Sep 2019, 11:41
J'ai essayé de jouer avec les inégalités triangulaires pour montrer que si a est valeur d'adhérence de un, alors pour tout e > 0, on obtient |a| < e mais il me reste toujours un terme qui bloque tout...
Pour le moment je ne me préoccupe pas du N dans la définition de la convergence avec les epsilons, on pourra le trouver par la suite.
J'ai tenté d'écrire :
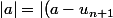 + (u_n - a) + (u_n^2 - u_n^2) + (a - u_n) + u_{n+1} |)
mais le u_n+1 à la fin m'embête ...
-
rog974
- Messages: 8
- Enregistré le: 11 Mar 2015, 19:05
-
 par rog974 » 14 Sep 2019, 13:04
par rog974 » 14 Sep 2019, 13:04
Le théorème de Bolzano-Weierstrass te dit-il quelque chose ?
-
Nanos
- Messages: 9
- Enregistré le: 14 Sep 2019, 10:37
-
 par Nanos » 14 Sep 2019, 13:11
par Nanos » 14 Sep 2019, 13:11
Oui et sa généralisation topologique : dans un espace métrique compact X, toute suite à valeur dans X possède au moins une sous-suite convergente. Comme (un) est bornée, on peut dire que (un) prend ses valeurs dans le compact [-M, M] (si M est bien sur la valeur qui borne un). Mais je ne vois pas comment prouver que les sous-suites convergentes de la suite convergent bien vers 0 et pas une autre valeur...
-
Nanos
- Messages: 9
- Enregistré le: 14 Sep 2019, 10:37
-
 par Nanos » 14 Sep 2019, 13:16
par Nanos » 14 Sep 2019, 13:16
Avec beaucoup d'aide d'un intervenant, j'y suis parvenu. Merci pour votre aide.
Bonne journée.
-
rog974
- Messages: 8
- Enregistré le: 11 Mar 2015, 19:05
-
 par rog974 » 14 Sep 2019, 13:17
par rog974 » 14 Sep 2019, 13:17
Comme
)
est bornée, d'après Bolzano-Weierstrass, il existe une sous-suite
)
qui converge vers

. Aussi, la suite
)
est une sous-suite de
)
.
Que peut-on en déduire sur la limite de
)
? Sur les valeurs possibles de

?
Oups, l'intervenant a résolu la question...
-
Nanos
- Messages: 9
- Enregistré le: 14 Sep 2019, 10:37
-
 par Nanos » 14 Sep 2019, 13:24
par Nanos » 14 Sep 2019, 13:24
Il n'y aucun problème, si d'autres personnes ont cet exercice, ils pourront bénéficier d'un guide

J'aurais dû justement mettre l'idée que vous venez d'écrire.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Sep 2019, 15:54
par Ben314 » 14 Sep 2019, 15:54
Salut,
Juste un mot pour signaler que ça :
rog974 a écrit:. . . il existe une sous-suite
)
qui converge vers

.
Aussi, la suite ) est une sous-suite de
est une sous-suite de )
.
c'est une énorme connerie.
Le fait que
_k)
soit une suite extraite de
_n)
signifie qu'il existe

strictement croissante telle que, pour tout

, on ait
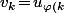)
.
Et si on prend
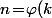)
dans l'expression

ça donne
+1}\!-\!u_{\varphi(k)}\!-\!u_{\varphi(k)}^2)
qui n'a aucune raison d'être égal à
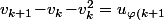}\!-\!u_{\varphi(k)}\!-\!u_{\varphi(k)}^2)
. (il n'y a bien sûr aucune raison que
\!=\!\varphi(k)\!+\!1)
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 14 Sep 2019, 16:09
par GaBuZoMeu » 14 Sep 2019, 16:09
Il mes semble qu'on peut raisonner sur

et

.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Sep 2019, 16:14
par Ben314 » 14 Sep 2019, 16:14
Pour moi, la façon la plus raisonnable de procéder, c'est ça :
Ensuite, si

est une des valeur d'adhérence de
_n)
alors il existe

strictement croissante telle que
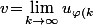})
ce qui implique que
}^2\!+\!u_{\varphi(k)}\!=\!v^2\!+\!v\ \ (*))
.
Or, le fait que

implique que
+1}\!-\!u_{\varphi(k)}^2\!-\!u_{\varphi(k)}\!=\!0)
ce qui, en sommant avec
)
nous dit que
+1}\!=\!v^2\!+\!v)
c'est à dire que

est aussi valeur d'adhérence de

.
L'ensemble

des valeurs d'adhérences de
_n)
est donc non vide (Bolzano-Weierstrass) ; borné (par les mêmes bornes que la suite elle-même) et stable par la fonction

.
On en déduit alors aisément que

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 14 Sep 2019, 16:56
par GaBuZoMeu » 14 Sep 2019, 16:56
Bah, ça revient en gros au même que le raisonnement avec

et

, non ? On a

si

, donc
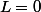
et on ne peut pas avoir

car dans ce cas si

alors

.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 14 Sep 2019, 17:27
par Ben314 » 14 Sep 2019, 17:27
GaBuZoMeu a écrit:Bah, ça revient en gros au même que le raisonnement avec

et

, non ?
Oui, c'est exactement la même chose modulo que c'est un soupçon plus court avec les limites sup et inf, mais que ça demande un soupçon plus de bagage. . .
Le problème en fait, c'est que j'ai mis plus de 5 minutes à taper mon laïus et que j'ai pas vérifié s'il y en avait un nouveau avant de l'envoyer . . . d'où la redondance . . .
Modifié en dernier par
Ben314 le 14 Sep 2019, 17:39, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 14 Sep 2019, 17:37
par GaBuZoMeu » 14 Sep 2019, 17:37
On est bien d'accord !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
