Limite et nombre premier

[mehdi-128]

Bonsoir,

Je bloque quelque peu sur cet exercice de mon livre qui comporte un étoile de difficulté. Je ne vois pas comment partir pour la 1.

Soit la fonction définie sur par :



1/ Démontrer que
2/ a-t-elle une limite en ?

[Yezu]

Salut,

La 1 est franchement très simple, c'est quoi la définition d'un nombre premier ?

[mehdi-128]

Un nombre qui admet exactement 2 diviseurs distincts entiers et positifs.

On a :

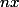
Il faut montrer que n'est pas premier quand ?

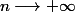
[mehdi-128]

1er cas :
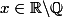
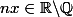
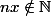
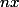
Si , alors donc . Ainsi ne peut pas être premier.
On obtient : et donc

2ème cas :
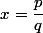
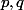
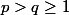
Si , posons avec premiers et car .
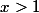
On a :
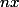
Comment trouver pour quelles valeurs de , est-il premier ?

[Kolis]

Tu crois vraiment que tu peux te contenter de chercher les limites sur deux parties disjointes ?

[GaBuZoMeu]

1er cas :
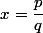
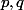
Si , posons avec premiers

Tu crois vraiment qu'un nombre rationnel est le quotient de deux nombres premiers ? Ne fais-tu pas une confusion avec "premiers entre eux" ?

[mehdi-128]

Tu crois vraiment que tu peux te contenter de chercher les limites sur deux parties disjointes ?

Non je cherche à calculer en fonction des valeurs de . Déjà pour irrationnel on voit que

Pour rationnel je suis un peu bloqué.

[mehdi-128]

@ GaBuZoMeu

Oui vous avez raison

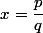
Si , posons avec 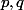premiers entre eux et
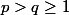
On a :
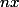
Comment trouver pour quelles valeurs de , est-il premier ?

S'il y en a un qu'on nombre fini, cela montre que pour un assez grand on aura

[GaBuZoMeu]

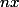
Comment trouver pour quelles valeurs de , est-il premier ?

En réfléchissant
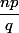
1°) Aux valeurs de pour lesquelles est entier (en utilisant le fait que et sont premiers entre eux).
2°) Aux conditions pour que cet entier soit premier.

[mehdi-128]

Merci !

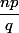
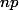
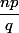
est entier si et seulement si divise . Or et sont premiers entre eux, d'après le théorème de Gauss, est entier si et seulement si divise .
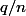
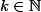
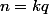
Si , alors il existe tel que : . Donc

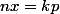Conditions pour avoir 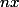premier.
Je sèche complètement

[Kolis]

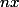
Tu trouves que est produit de deux entiers et tu te demandes s'il est premier ?

[mehdi-128]

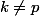
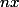
Si alors n'est pas premier car c'est le produit de 2 entiers distincts.

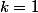
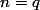
Si alors est peut être premier si est premier.

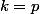
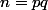
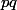
Si alors il peut être premier si le produit est premier.

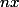
Donc est premier pour au plus 2 valeurs de .

Sauf que dans mon livre, il est écrit qu'il est premier pour au plus une valeur de je n'ai pas compris...

[GaBuZoMeu]

1 x 7 est le produit de deux entiers distincts, donc il n'est pas premier ?

Reprends tout le discours de ton dernier message, ça ne va pas du tout.

[mehdi-128]

Je n'ai pas compris comment faire

[GaBuZoMeu]

Récapitulons.
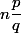
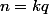
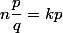
Tu as vu que si est entier, alors il existe un entier tel que . Dans ce cas, à quelle condition est il premier ?

[mehdi-128]

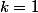
et premier ?

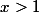
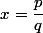
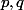
Fixons . Si on pose et sont donc fixés.
La condition imposée sur est .

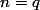
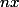
Si est premier il existe exactement une valeur de pour laquelle est premier.

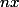
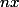
Si n'est pas premier alors n'est pas premier. Il n'y a aucune valeur de pour laquelle est premier.

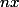
Il existe donc au plus une valeur de pour laquelle est premier.

[GaBuZoMeu]

C'est presque complet, il serait bon de rappeler l'argument qui élimine le cas p=1, k premier.

[mehdi-128]

Si p=1 et k premier alors x=1/q ce qui est impossible car x>1 et q est entier.

[GaBuZoMeu]

Voila. On voit bien le rôle de l'hypothèse .

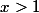
[mehdi-128]

Merci