Continuité

[mehdi-128]

Bonsoir,

Soit

1/ Démontrer que pour tout , la fonction est uniformément continue.
Pour tout
est lipschitzienne elle est donc uniformément continue.

2/ Soit . Montrer qu'il existe un réel tel que
Je n'ai pas trouvé.

3/ La fonction est-elle uniformément continue ?
Je ne vois pas non plus.

[Tuvasbien]

Pour le 2), la fonction est un polynôme du second degré... Pour la 3) la réponse est non, la définition de l'uniforme continuité c'est

donc pour montrer que f est pas uniformément continue il suffit de trouver deux suites et telles que et pour une infinité d'entiers et pour un certain .

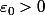
[Kolis]

Pour 2) il suffit de prendre .

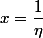
Cette réponse permet de résoudre 3)

[mehdi-128]

Pour la 3, je n'ai pas vu cette propriété dans le cours. Il n'y a aucune propriété qui relie suite et continuité uniforme dans le chapitre. Elle est peut être vue en MP...

Merci pour la 2 j'ai compris. Sinon je pense avoir trouvé une autre méthode :
Donc
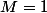
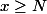
En prenant il existe bien un réel tel que pour tout on a : . Il existe donc un réel tel que .

J'essaie d'utiliser la définition. Il faut montrer que :



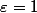
Prenons . Soit
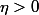
Prenons tel que
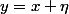
Prenons on a bien

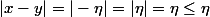
Il suffit de montrer que
On a :

[mehdi-128]

Pour 2) il suffit de prendre .

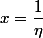
Cette réponse permet de résoudre 3)

Bien vu c'est beaucoup plus rapide que ce que j'ai fait

[Tuvasbien]

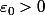
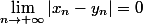
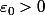
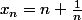
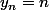
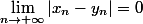
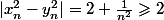
Je suis sûr que cette propriété est dans le cours, de la même façon que la caractérisation séquentielle de la continuité y est également, dire que n'est pas uniformément continue, c'est dire qu'il existe tel que et . S'il existe et telles que et pour un certain , alors on a montré que n'est pas uniformément continue. Pour en revenir à , si on pose et , alors et donc n'est pas uniformément continue sur .

[mehdi-128]

En effet, c'est souvent plus rapide avec les suites, la méthode est sympa.

Dans mon livre, il y a la caractérisation séquentielle de la continuité oui mais pour la continuité uniforme il n'y a rien.

Mais le principal c'est d'arriver à destination

[LB2]

Tu as vu la démonstration du théorème de Heine ? On utilise souvent les suites dedans.