Fonction réciproque
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 10 Sep 2019, 10:53
par Ncdk » 10 Sep 2019, 10:53
Bonjour,
Enoncé : Expliquer comment on peut retrouver la formule donnant
'(b))
en supposant

dérivable et en calculant la dérivée de
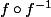
ou de
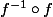
.
Soit
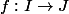
)=x)
Soit
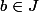
,
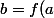)
'(b)=f'(f^{-1}(b)) \times (f^{-1})'(b)=f'(a) \times (f^{-1})'(b))
Du coup, il me manque deux justifications que je n'arrive pas à expliquer ou surement maladroitement.
'(b)=1)
car
'(b)=Id'(b)=1)
car
=b)
 \neq 0)
, pourquoi ?
Merci d'avance !
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 10 Sep 2019, 11:29
par lyceen95 » 10 Sep 2019, 11:29
Tu as supposé

dérivable. Donc
')
est définie, et comme
' * f' = 1)
, forcément f' ne peut pas s'annuler.
Si tu veux une illustration, prend la fonction f(x)=x². Elle est dérivable , mais sa dérivée vaut 0 quand x vaut 0.
La fonction inverse est la fonction racine carrée. Et à cause de cette dérivée nulle pour f(x)=x², la fonction racine carrée n'est pas dérivable quand x=0.

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 10 Sep 2019, 11:37
par Ncdk » 10 Sep 2019, 11:37
Ah oui super !
Merci pour l'exemple.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités