Bijection
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 08 Sep 2019, 20:57
par mehdi-128 » 08 Sep 2019, 20:57
Bonsoir,
Démontrer que la fonction définie sur  par
par =\begin{cases} x \ \text{si} \ x \in ]0,1[ \\ x-1 \ \text{si} \ x \in [2,3[ \\ \end{cases}) définit une bijection continue strictement croissante de son domaine de définition sur
définit une bijection continue strictement croissante de son domaine de définition sur 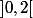 . Son application réciproque est-elle continue ?
. Son application réciproque est-elle continue ? 
est continue sur

et pour la stricte croissante il suffit d'étudier les cas suivants :
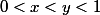
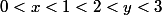
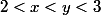
Par contre comment déterminer
 = ]0,2[)
alors que

n'est pas un intervalle ?
Dans mon cours, on donne les images d'intervalle par une fonction continue mais ci ça ne s'applique pas...
Modifié en dernier par
mehdi-128 le 08 Sep 2019, 22:32, modifié 1 fois.
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 08 Sep 2019, 21:22
par Tuvasbien » 08 Sep 2019, 21:22
Le mieux est de tracer le graphe de la fonction, je pense que tracer le graphe justifie complètement ta réponse
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 08 Sep 2019, 21:34
par mehdi-128 » 08 Sep 2019, 21:34
Ok merci. Ensuite je dois déterminer

qui est définie sur
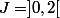
=\begin{cases} x \ \text{si} \ x \in ]0,1[ \\ x-1 \ \text{si} \ x \in ]2,3[ \\ \end{cases})
Soit
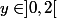
. Normalement je dois résoudre
=y)
mais comment faire avec une fonction définie avec une accolade ?
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 08 Sep 2019, 22:05
par Tuvasbien » 08 Sep 2019, 22:05
Il y a une erreur, l'image de

est

, on voit sur le graphe que

induit une bijection de
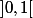
dans
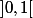
et une bijection de
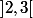
dans
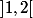
donc il faut définir

par morceaux : si
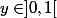
,
=\ldots)
et si
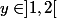
, alors
=\ldots)
.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 08 Sep 2019, 22:30
par mehdi-128 » 08 Sep 2019, 22:30
Excusez moi j'ai corrigé ma coquille, l'intervalle est bien fermé en 2 dans la définition de

On a
=\begin{cases} x \ \text{si} \ x \in ]0,1[ \\ x-1 \ \text{si} \ x \in [2,3[ \\ \end{cases})
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 08 Sep 2019, 22:41
par mehdi-128 » 08 Sep 2019, 22:41
Soit
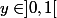
. Ainsi
=y \Leftrightarrow x=y)
car
 \in ]0,1[ \Leftrightarrow x \in ]0,1[)
Soit
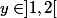
. Ainsi
=y \Leftrightarrow x=y+1)
car
 \in ]1,2[ \Leftrightarrow y \in ]1,2[)
Ainsi :
=\begin{cases} y \ \text{si} \ y \in ]0,1[ \\ y+1 \ \text{si} \ y \in ]1,2[ \\ \end{cases})
On remarque que
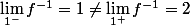
donc

n'est pas continue en

. Elle n'est donc pas continue sur
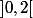
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 09 Sep 2019, 08:59
par LB2 » 09 Sep 2019, 08:59
Réponse ultrarapide : tu traces le graphe de f. Tu tournes la feuille de 90° et tu vois que sa réciproque "saute" en 1 donc elle n'est pas continue.
Ceci ne remplace bien sûr pas une démonstration
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités