Bonjour,
Dans des exercices que j'ai à faire, je dois calculer des dérivées n-ièmes.
Voici une des dérivées n-ièmes que j'ai à calculer :
1) sin(x)e^x
Dans la correction, la solution est √2^n*exp(x)*sin(x+npi/4)
or j'ai beau refaire le calcul le temre √2^n n'apparait pas
Merci de votre aide
Derive n-ème
8 messages
- Page 1 sur 1
Re: Derive n-ème
slt,
on remarque d'abord
 = \frac{\sqrt{2}}{2}(\sin(x) + \cos(x)))
et on déduit
 + \cos(x) = a\sin(x+ \frac{\pi}{4}))
avec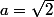
 = \sin(x)e^x)
 = e^x(\sin(x)+\cos(x)) = ae^x\sin(x + \frac{\pi}{4}))
puis on intuite
 = a^ne^x\sin(x+ n \frac{\pi}{4}))
puis récurrence
on remarque d'abord
et on déduit
avec
puis on intuite
puis récurrence
la vie est une fête 
Re: Derive n-ème
Merci de votre réponse, j'ai une autre dérive n-eme qui me pose problème
(x^3+x^2+1)*exp(-x)
j'ai pensé a la formule de leibniz cependant quand on dérive (x^3+x^2+1) 4 fois ou plus la dérivée est nul donc le terme dans la somme est nul mais je n'arrive pas trouvé de formule en fonction de n
(x^3+x^2+1)*exp(-x)
j'ai pensé a la formule de leibniz cependant quand on dérive (x^3+x^2+1) 4 fois ou plus la dérivée est nul donc le terme dans la somme est nul mais je n'arrive pas trouvé de formule en fonction de n
Re: Derive n-ème
Un détour qui demande un peu de connaissance, est de voir que \,\exp(x)) est la partie imaginaire de
est la partie imaginaire de \,\exp(x)=\exp((1+i)x)) .
.
La dérivée -ème de
-ème de ) se calcule facilement : c'est
se calcule facilement : c'est ) .
.
Il ne reste plus qu'à trouver la partie imaginaire de^n\exp((1+i)x)) . On peut se souvenir que
. On peut se souvenir que 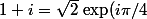) .
.
La dérivée
Il ne reste plus qu'à trouver la partie imaginaire de
Re: Derive n-ème
Este a écrit:j'ai pensé a la formule de Leibniz cependant quand on dérive (x^3+x^2+1) 4 fois ou plus la dérivée est nul donc le terme dans la somme est nul
Très bon réflexe. Et tant mieux si beaucoup de termes sont nuls, on n'a dans la formule que les termes avec
Re: Derive n-ème
C'est ce que j'ai fait sauf qu'on nous demande la dérivée en fonction de n, j'ai essayé avec 4 par exemple mais ensuite je n'arrive pas a trouvé une formule en fonction de n
Re: Derive n-ème
Este a écrit:C'est ce que j'ai fait sauf qu'on nous demande la dérivée en fonction de n, j'ai essayé avec 4 par exemple mais ensuite je n'arrive pas a trouvé une formule en fonction de n
Vraiment ?? La formule de Leibniz te donne ça, pourtant.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
