Fonction lipschitzienne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Aoû 2019, 02:34
par mehdi-128 » 27 Aoû 2019, 02:34
Bonsoir,
Il est écrit dans mon livre pour la correction d'un exercice concernant la fonction
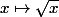
Si

est lipschitzienne, l'ensemble
-f(x)|}{|y-x|} ; (x,y) \in \R^{+2} , x \ne y \})
serait borné.
Déjà il suffit pas de dire majoré ? Je n'ai pas compris pourquoi il faut le "borné".
Comme
-f(x)}{2x-x} \right| =3x)
la fonction n'est pas lipschitzienne.
Je n'ai pas compris pourquoi si on a
-f(x)}{2x-x} \right| =3x)
, l'ensemble ci-haut n'est pas borné...
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 27 Aoû 2019, 07:17
par GaBuZoMeu » 27 Aoû 2019, 07:17
Ça m'étonnerait beaucoup qu'il soit écrit dans ton livre que
-f(x)}{2x-x}\right| =3x)
si

est la fonction
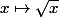
.

-
vam
- Admin
- Messages: 680
- Enregistré le: 09 Aoû 2019, 09:50
-
 par vam » 27 Aoû 2019, 07:19
par vam » 27 Aoû 2019, 07:19
Bonjour
et tu montres comment tu trouves 3x ?
Pour mettre une image, vous pouvez aller sur
https://postimages.org/fr/Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

-
henryallen
- Membre Naturel
- Messages: 18
- Enregistré le: 07 Aoû 2019, 12:26
-
 par henryallen » 27 Aoû 2019, 13:31
par henryallen » 27 Aoû 2019, 13:31
Bonjour,
Si on omet l'incohérence déjà évoquée, pour répondre aux questions:
-Oui, dire majoré suffit dans la mesure où on remarque facilement que l'ensemble étudié est dans tous les cas minoré (par 0 par exemple). Mais dire borné montre bien qu'on l'a remarqué.
-Si on a cette égalité, il est évident qu'en prenant un x suffisamment grand, et en posant y = 2x, alors
 - f(x)}{y - x}|)
est aussi grand que l'on veut, et donc l'ensemble n'est pas majoré.
Bonne journée.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Aoû 2019, 13:44
par mehdi-128 » 27 Aoû 2019, 13:44
Excusez moi pour cette erreur c'est la fonction
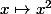
définie sur

et c'est :
-f(x)}{2x-x}\right| =3x)
Dire que la fonction
-f(x)}{2x-x})
est bornée c'est dire que :
-f(x)}{2x-x}\right| \leq M)
Donc dire qu'elle n'est pas bornée c'est dire que :

et comme
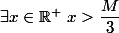
elle n'est pas bornée. Il suffit de prendre
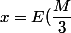+1)
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 27 Aoû 2019, 17:04
par Kolis » 27 Aoû 2019, 17:04
Quelle rédaction biscornue !
D'abord, tu annonces que tu veux un réel

supérieur à

puis tu te contentes d'en trouver un supérieur à
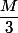
! Où est le bon

?
De plus ta démonstration est incorrecte : on ne cherche pas
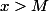
mais un réel

tel que
-f(x)}{2x-x}>M\cdot)
Ne serait-ce pas plus simple de choisir
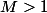
et alors tu as bien
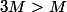
en notant que l'inégalité stricte est même inutile ?
Tu trouves sans doute que tu n'as pas eu assez de déboires avec les parties entières !
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Aoû 2019, 17:13
par mehdi-128 » 27 Aoû 2019, 17:13
On ne peut pas choisir
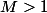
, pour montrer qu'une fonction n'est pas bornée, il faut le montrer quelque soit
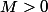
.
Soit
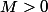
. On cherche un réel

tel que
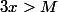
Il suffit de prendre
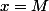
on a bien
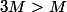
car
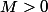
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 27 Aoû 2019, 17:17
par Tuvasbien » 27 Aoû 2019, 17:17
Franchement c’est ridicule, pourquoi autant de formalisme pour montrer que l’ensemble
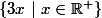
est pas majorée...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Aoû 2019, 17:48
par mehdi-128 » 27 Aoû 2019, 17:48
Tuvasbien a écrit:Franchement c’est ridicule, pourquoi autant de formalisme pour montrer que l’ensemble
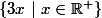
est pas majorée...
Il suffit de dire que
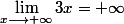
?
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 27 Aoû 2019, 18:01
par Tuvasbien » 27 Aoû 2019, 18:01
Bien sûr, une partie majorée de

c'est une partie qui n'excède pas une valeur (un majorant), si une partie de

peut prendre des valeurs arbitrairement grandes alors elle peut pas être majorée, c'est bien pour comprendre le français parfois (souvent).
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 27 Aoû 2019, 19:26
par Kolis » 27 Aoû 2019, 19:26
mehdi-128 a écrit:On ne peut pas choisir
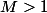
, pour montrer qu'une fonction n'est pas bornée, il faut le montrer quelque soit
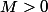
.
Soit
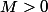
. On cherche un réel

tel que
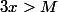
Il suffit de prendre
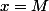
on a bien
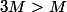
car
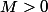
Vas-tu finir par réaliser que si tu montres que tous les réels supérieurs à 1 ne sont pas majorants alors, tout réel n'est pas majorant ?
Et comme tu dois montrer qu'une valeur absolue n'est pas bornée, il est évident qu'il suffit de montrer qu'elle n'est pas majorée.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Aoû 2019, 20:10
par mehdi-128 » 27 Aoû 2019, 20:10
Kolis a écrit: mehdi-128 a écrit:On ne peut pas choisir
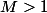
, pour montrer qu'une fonction n'est pas bornée, il faut le montrer quelque soit
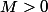
.
Soit
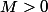
. On cherche un réel

tel que
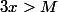
Il suffit de prendre
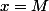
on a bien
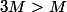
car
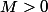
Vas-tu finir par réaliser que si tu montres que tous les réels supérieurs à 1 ne sont pas majorants alors, tout réel n'est pas majorant ?
Et comme tu dois montrer qu'une valeur absolue n'est pas bornée, il est évident qu'il suffit de montrer qu'elle n'est pas majorée.
Ah oui en effet merci.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 131 invités
est pas majorée...
, pour montrer qu'une fonction n'est pas bornée, il faut le montrer quelque soit
.
. On cherche un réel
tel que
on a bien
car
, pour montrer qu'une fonction n'est pas bornée, il faut le montrer quelque soit
.
. On cherche un réel
tel que
on a bien
car